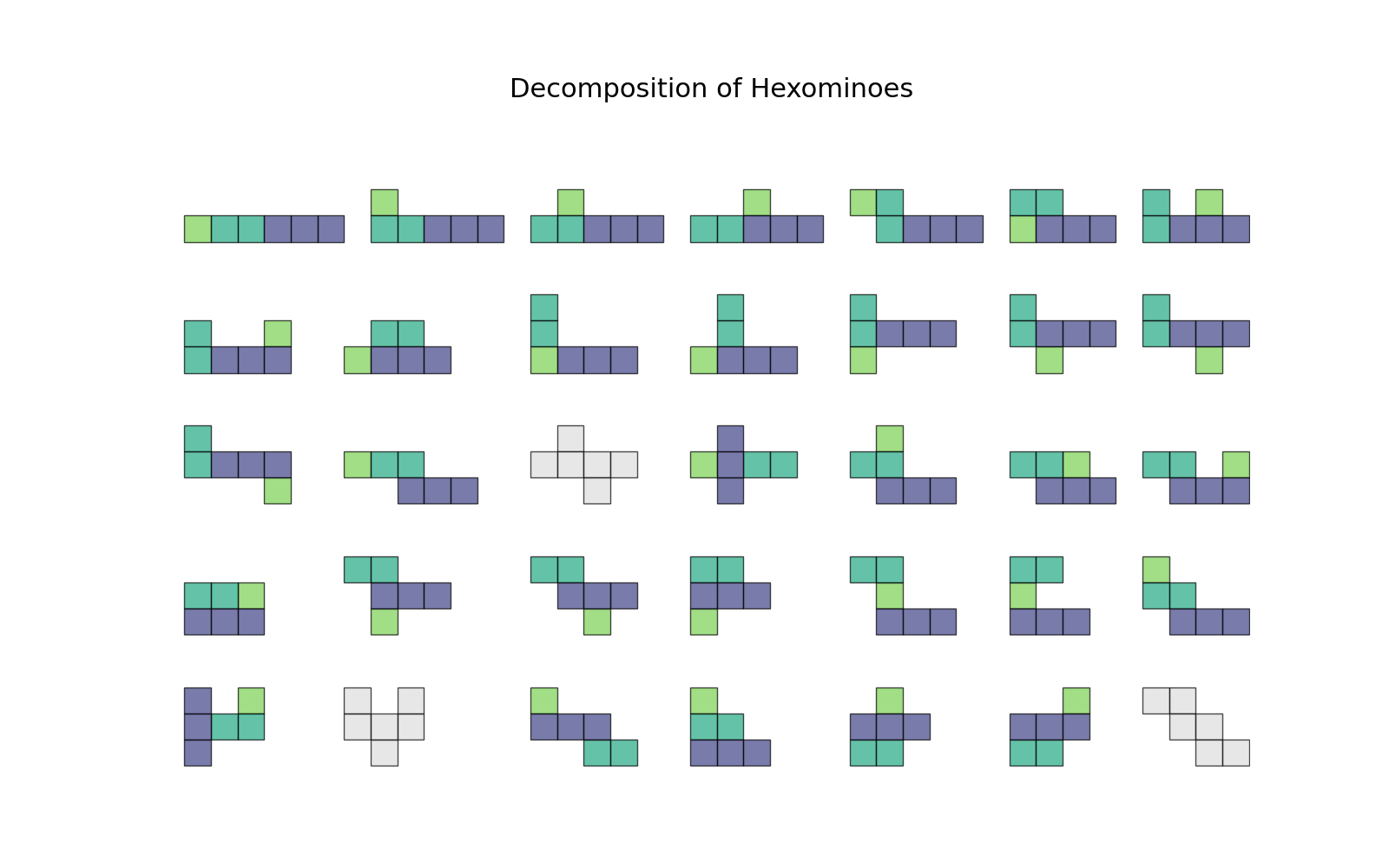
Can You Decompose the Hexominoes?¶
Riddler Express¶
Earlier this week, I had the pleasure of attending the MOVES conference in New York City, hosted by the National Museum of Mathematics. The opening keynote, “How to Invent Puzzles,” was delivered by puzzle master Scott Kim. In particular, his cuisenaire-rod puzzles got me thinking. …
A hexomino is a shape made by six identical, nonoverlapping squares that are connected by edges. Some hexominoes, like the one shown below, can be decomposed into an array of three squares, an array of two squares and an array of one square.

How many distinct hexominoes can you find that cannot be decomposed into arrays of three, two and one squares? For the purposes of this riddle, two hexominoes are considered equivalent if they can be turned into one another by rotation and/or reflection.