You can generate a heart shape by drawing a unit square (i.e., a square with side length 1), and then attaching semicircles (each with radius 1/2) to adjacent edges, as shown in the diagram below:
What is the radius of the smallest circle that contains this heart shape?
The point of tangency, $T$ can be drawn to the center of a semicircicle, $V$, and center of the large circle, $C$, and $V$ lies on $TC$. The following lengths are easily determined:
Applying Stewart's Theorem to $\bigtriangleup VWX$,
\begin{align*} CW\cdot VX^2 + CX\cdot VW^2 &= CW\cdot CX \cdot WX + CV^2 \cdot WX \\ (\sqrt{2} - r)\cdot \bigg(\frac{\sqrt{5}}{2}\bigg)^2 + r\cdot \bigg(\frac{1}{2}\bigg)^2 &= r\cdot (\sqrt{2} - r) \cdot r \cdot \sqrt{2} + \left(r-\frac{1}{2}\right)^2 \cdot \sqrt{2} \\ \bigg(\frac{5\sqrt{2}}{4} - \frac{5}{4}r\bigg) + \bigg(\frac{r}{4}\bigg) &= \bigg(-\sqrt{2}r^2 + 2r\bigg) + \bigg(\sqrt{2}r^2 -\sqrt{2}r +\frac{\sqrt{2}}{4}\bigg) \\ \frac{5\sqrt{2}}{4} - r &= (2-\sqrt{2})r +\frac{\sqrt{2}}{4} \\ \sqrt{2} &= (3-\sqrt{2})r \\ \end{align*}Instead of containing one heart shape, now your circle must contain two heart shapes. Again, each heart consists of a unit square and two semicircular lobes. The two hearts are not allowed to overlap.
What is the radius of the smallest circle that contains these two hearts?
The radius is at least the diagonal of the square, $\sqrt{2}$, and at most the distance from the center of a semicircle to the center of the opposite base of the square, $\frac{3}{2}$.
I looked at a few possibilities. Symmetry is inevitable. I thought utilizing the region near the top cusp of the heart would be useful, so I first tried stacking the hearts vertically.
The point of tangency, $T$ can be drawn to the center of a semicircicle, $U$, and center of the large circle, $C$, and $U$ lies on $TC$.
$UV = \frac{1}{2}$, so $UW = WV = \frac{1}{\sqrt{8}}$. Let $CU = q$, $CW = \sqrt{q^2 - \frac{1}{8}}$.
Since all radii are equal,
\begin{align*} CT &= CY \\ CU + UT &= VY - CW - VW \\ q + \frac{1}{2} &= 2\sqrt{2} - \sqrt{q^2 - \frac{1}{8}} - \frac{1}{\sqrt{8}} \\ q + \sqrt{q^2 - \frac{1}{8}} &= \sqrt{8} - \frac{1}{2} - \frac{1}{\sqrt{8}} \\ \left(q + \sqrt{q^2 - \frac{1}{8}}\right)^2 &= \left(\frac{8-1-\sqrt{2}}{\sqrt{8}}\right)^2 \\ q^2 + q^2 - \frac{1}{8} + 2q\sqrt{q^2 - \frac{1}{8}} &= \frac{49+2-14\sqrt{2}}{8} \\ 2q\sqrt{q^2 - \frac{1}{8}} &= -2q^2 + \frac{52-14\sqrt{2}}{8} \\ \left(8q\sqrt{q^2 - \frac{1}{8}}\right) &= \left(-8q^2 + 26-7\sqrt{2}\right) \\ 64q^4 - 8q^2 &= 64q^4 - 16q^2\left(26-7\sqrt{2}\right) + \left(26-7\sqrt{2}\right)^2 \\ 8q^2\left(52-14\sqrt{2}\right) - 8q^2 &= 8q^2\left(51-14\sqrt{2}\right) = \left(26-7\sqrt{2}\right)^2 \\ 4q^2 &= \frac{\left(26-7\sqrt{2}\right)^2}{102-28\sqrt{2}} \\ q &= \frac{26-7\sqrt{2}}{2\sqrt{102-28\sqrt{2}}} \\ r &= \boxed{q+\frac{1}{2} \approx 1.519} \end{align*}This is not optimal.
I looked at $180^\circ$ rotational symmetry. Both cusp regions are partially utilized by one of the other heart's semicircles.
The point of tangency of a semicircicle from each heart and the center of the large circle is $C$. $U$ and $V$ are centers of semicircles.
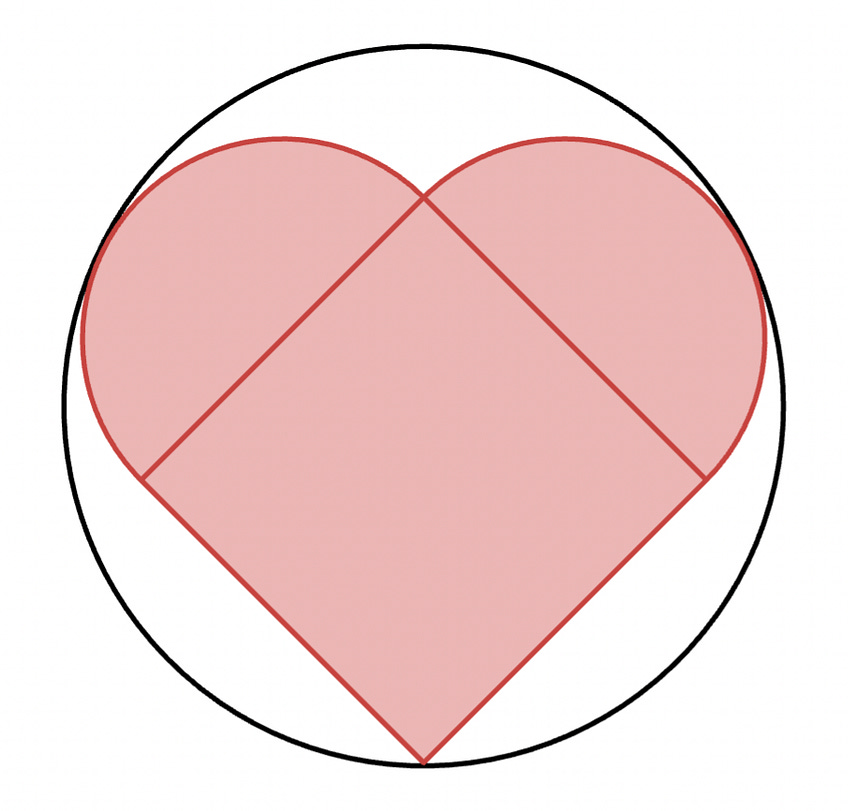
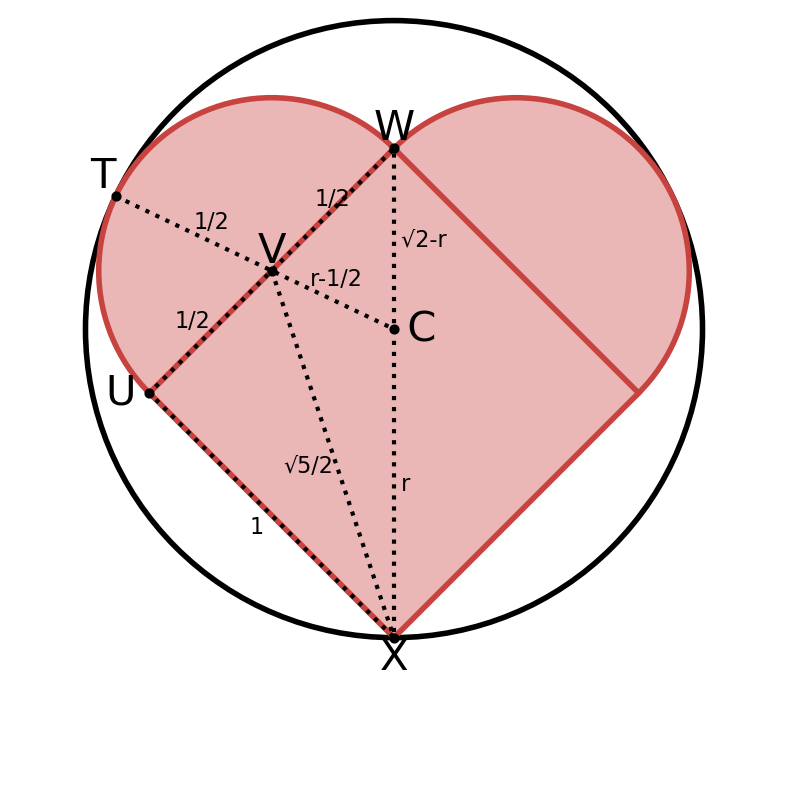
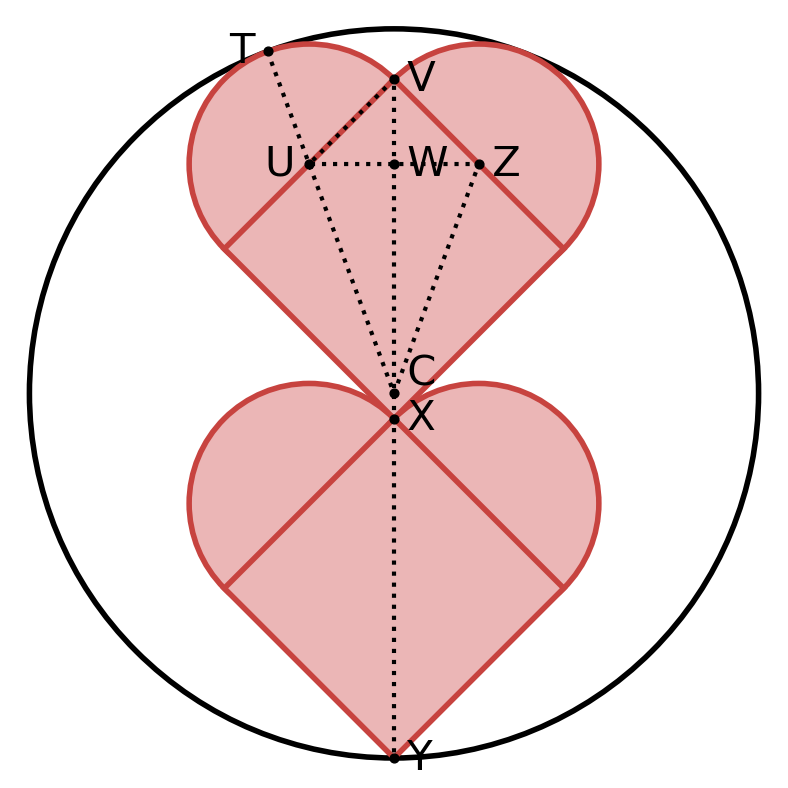
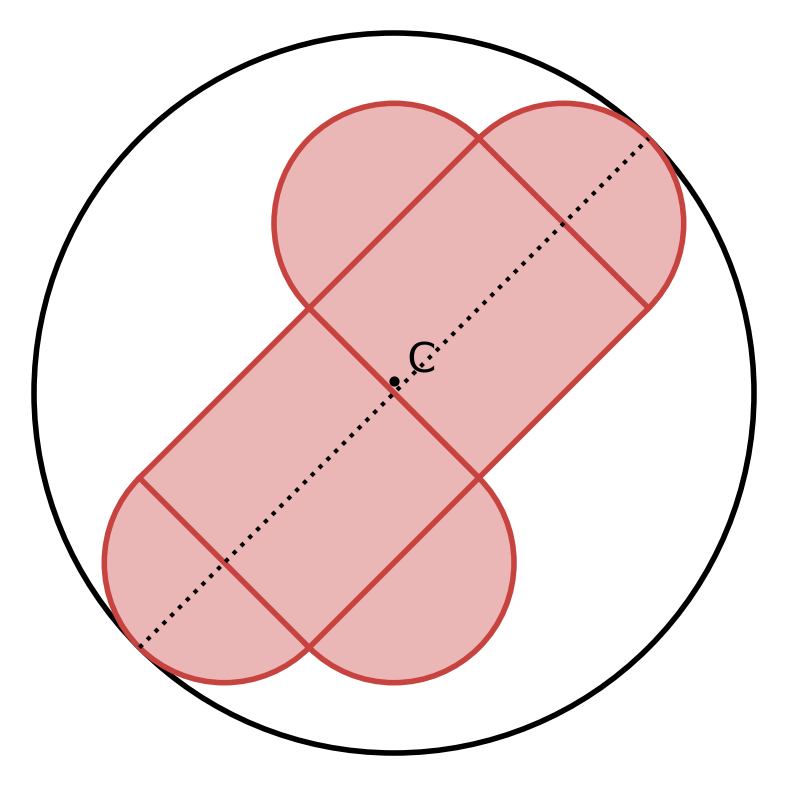
Because of symmetry, $\bigtriangleup CUT \cong \bigtriangleup CVW$.
$UX = \frac{1}{2}$, $TW = UY = XY = \frac{1}{\sqrt{8}}$, and $CT = CW = \frac{1}{\sqrt{32}}$.
$UT = WY$.
\begin{align*} UT^2 &= CU^2 - CT^2 \\ WY &= \sqrt{\left(\frac{1}{2}\right)^2 - \left(\frac{1}{\sqrt{32}}\right)^2} = \sqrt{\frac{7}{32}} \\ \end{align*}$\bigtriangleup CWZ$ (radius $CZ$ not drawn),
\begin{align*} CZ^2 &= WZ^2 + CW^2 \\ r^2 &= (WY + YZ)^2 + CW^2 \\ r^2 &= \big(UT + (XZ-XY)\big)^2 + CW^2 \\ r &= \sqrt{\left(\sqrt{\frac{7}{32}} + \left(\sqrt{2}-\frac{1}{\sqrt{8}})\right)\right)^2 + \left(\frac{1}{\sqrt{32}}\right)^2} \\ r &= \sqrt{\left(\sqrt{\frac{7}{32}} + \left(\frac{3}{\sqrt{8}}\right)\right)^2 + \left(\frac{1}{32}\right)} \\ r &= \sqrt{\left(\frac{6+\sqrt{7}}{\sqrt{32}}\right)^2 + \frac{1}{32}} \\ r &= \sqrt{\frac{36+12\sqrt{7}+7+1}{32}} \\ r &= \boxed{\frac{\sqrt{22+6\sqrt{7}}}{4} \approx 1.5385}\\ \end{align*}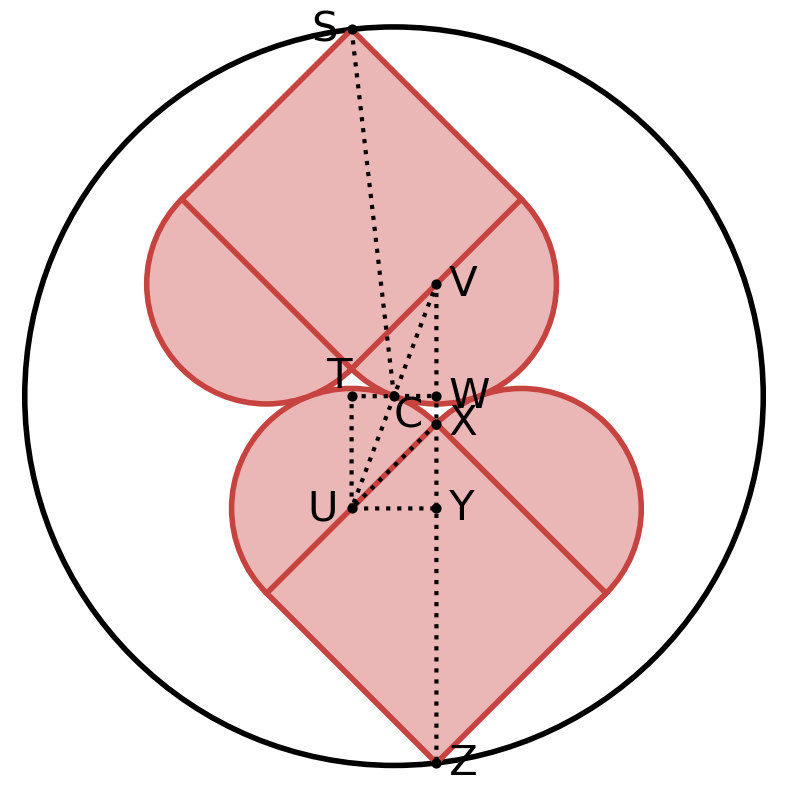This also is not optimal.
