What’s the Area of a “Pseudo-Square”?

Fiddler

From Tom Keith comes an opportunity to “square the circle,” so to speak:

A post from Anthony Bonato recently caught Tom’s attention. Here’s the image from that post:

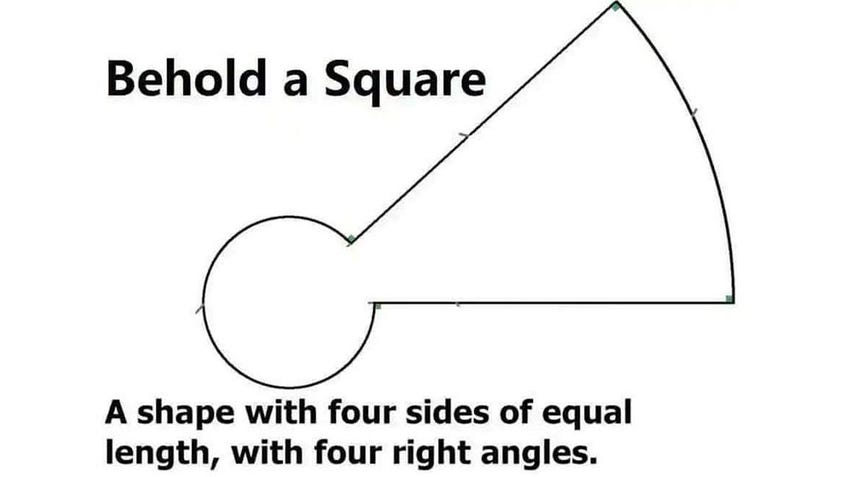
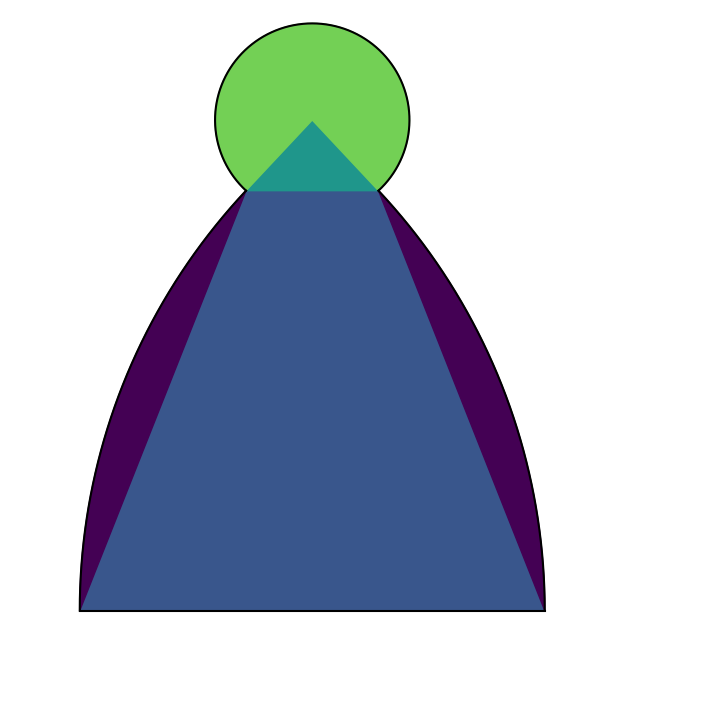
Sure enough, the shape (or one very much like it) has four “sides” of equal length, with four right angles. However, two of these sides are curved (in particular, they are arcs of circles), and two of the right angles are exterior, meaning the interior angles measure 270 degrees (rather than the usual 90 degrees).

Let’s call shapes like this one “pseudo-squares.” A pseudo-square has the following properties:

• It is a simple, closed curve.

• It has four sides, all the same length.

• Each side is either a straight line segment or the arc of a circle.

• The four sides are joined at four corners, with each corner having an internal angle of 90 degrees or 270 degrees.

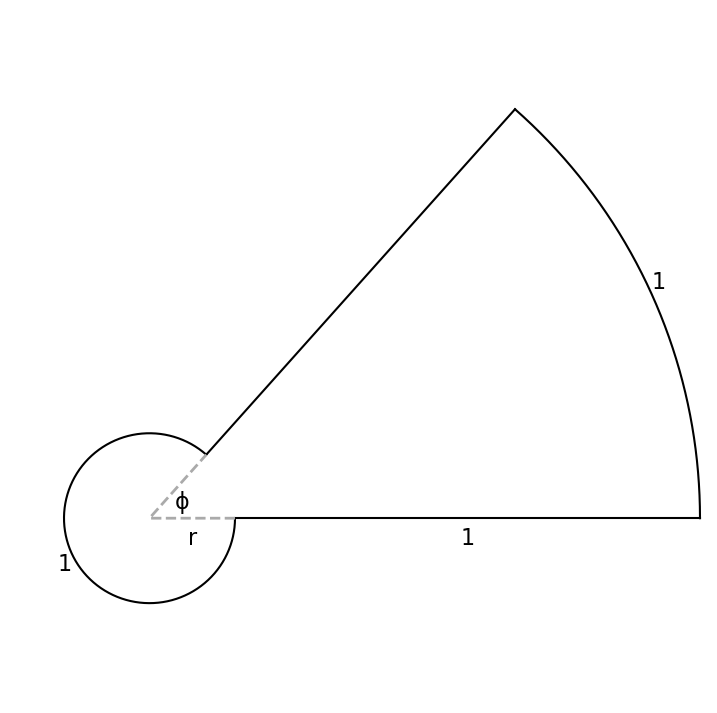
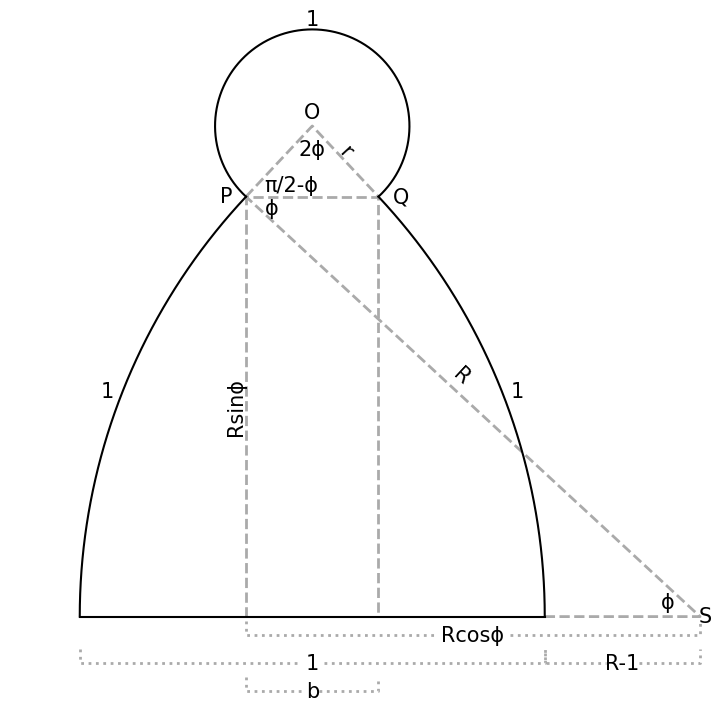
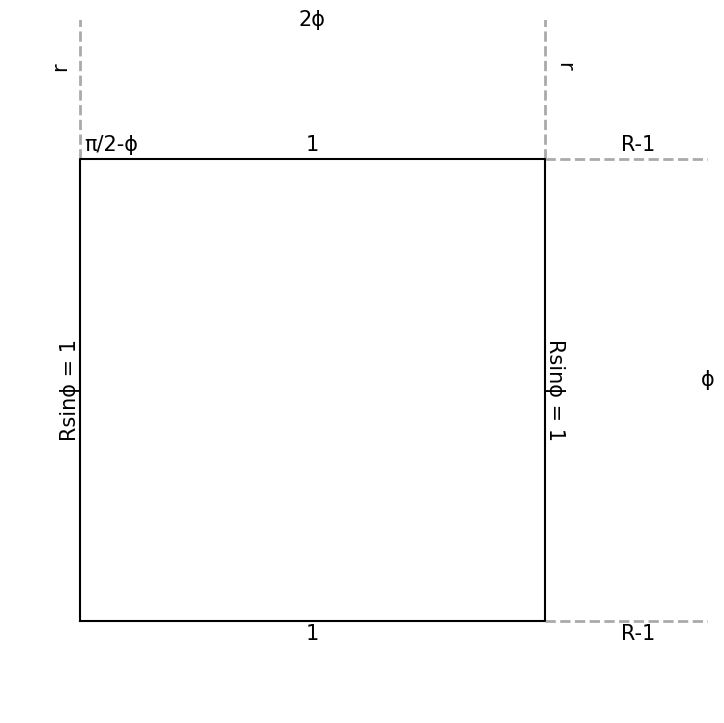
The pseudo-square pictured above has two straight sides, which run radially between arcs of two concentric circles.

Assuming this is a unit pseudo-square (i.e., each side has length 1), what is its area?

Solution

In the diagram above:

Knowing the major arc of the small circle is $1$,

$$\frac{2\pi r}{2\pi} = \frac{1}{2\pi - \phi}$$
$$\boxed{r = \frac{1}{2\pi - \phi}} $$

Knowing the minor arc of the large circle is $1$,
$$\frac{2\pi (r+1)}{2\pi} = \frac{1}{\phi}$$
$$\boxed{r = \frac{1}{\phi}-1}$$

Setting the two equal to each other,
$$\frac{1}{2\pi - \phi} = \frac{1}{\phi}-1$$
$$\phi = (2\pi - \phi) - (2\pi - \phi)\phi$$
$$0 = \phi^2 - (2\pi + 2)\phi +2pi$$
$$\phi = \frac{(2\pi + 2) \pm \sqrt{(2\pi + 2)^2 -(4)(1)(2\pi)}}{2}$$
$$\phi = \frac{2\pi + 2 \pm \sqrt{4\pi^2 + 8\pi + 4 - 8\pi}}{2}$$
$$\boxed{\phi = \pi + 1 - \sqrt{\pi^2 + 1} \approx 0.84468}$$

Solving for r,

$$\boxed{r \approx \frac{1}{0.84468} - 1\approx 0.1839}$$

The area can be determined from the solved variables and dividing the figure into the two sectors below.

The area can be found as follows:

• Left, Major Arc Sector

  • Angle = $2\pi - \phi$
  • Radius = $r$
  • Area = $\dfrac{2\pi - \phi}{2\pi} \cdot \pi r^2 = \boxed{\pi r^2 - \dfrac{r^2\phi}{2}}$



• Right, Minor Arc Sector

  • Angle = $\phi$
  • Radius = $r+1$
  • Area = $\dfrac{\phi}{2\pi} \cdot \pi (r+1)^2 = \boxed{\dfrac{r^2\phi}{2} + r\phi + \frac{\phi}{2}}$

$$A = \left(\pi r^2 - \frac{r^2\phi}{2}\right) + \left(\frac{r^2\phi}{2} + r\phi + \frac{\phi}{2}\right)$$

$$A = \pi r^2 + \phi\left(r + \frac{1}{2}\right)$$
$$A \approx \pi \cdot 0.1839^2 + 0.84468(0.1839+0.5)$$

Answer

$$\boxed{A \approx 0.6839}$$

---

Extra Credit

Hopefully, by this point, you have determined the area of a unit pseudo-square with two curved sides and two straight sides.

Can you find a unit pseudo-square that has three curved sides and just one straight side?

What is the area of your new unit pseudo-square?

Solution

In the diagram above:

Knowing the major arc of $\bigcirc O$ is $1$,

$$\frac{2\pi r}{2\pi} = \frac{1}{2\pi - 2\phi}$$
$$\boxed{r = \frac{1}{2\pi - 2\phi}} $$

Knowing the minor arc of $\bigcirc S$ is $1$,
$$\frac{2\pi R}{2\pi} = \frac{1}{\phi}$$
$$\boxed{R = \frac{1}{\phi}}$$

A third equation relating some combination of $\phi$, $r$, and $R$ is needed, and this comes from $b$. If the base of the figure were extended left to the center of the right arc, the length of the base can be expressed two ways and set equal.
$$(R-1) + 1 + (R-1) = R\cos \phi - b + R\cos \phi$$
$$b = 1+ 2R\cos \phi - 2R$$

Now, using Law of Sines on $\bigtriangleup OPQ$,
$$\frac{\sin(\frac{\pi}{2}-\phi)}{r} = \frac{\sin2\phi}{1+ 2R\cos \phi - 2R}$$
Cross-multiplying and simplifying with trigonometric identities,
$$\cos\phi\left(1+ 2R\cos \phi - 2R \right) = 2r\sin\phi\cos\phi$$
Substituting for $r$ and $R$ from above,
$$\cos\phi\left(1+ \frac{2\cos \phi - 2}{\phi}\right) = \frac{2\sin\phi\cos\phi}{2\pi - 2\phi}$$
$$\cos\phi\left(1 + \frac{2\cos \phi - 2}{\phi} - \frac{\sin\phi}{\pi - \phi}\right) = 0**$$

$\phi = \frac{\pi}{2}$ does not make sense, so using Desmos, $\phi \approx 0.7496$.

Solving for $r$,

$$\boxed{r \approx \frac{1}{2\pi - 2\cdot 0.7496} \approx 0.2090}$$

Solving for $R$,

$$\boxed{R \approx \frac{1}{0.7496} \approx 1.3340}$$

The area can be found as follows:

• Left & Right Circular Segments

  • Angle = $\phi$
  • Radius = $R$
  • Area = $2 \cdot \frac{1}{2}R^2(\phi - \sin \phi) = R - R^2\sin\phi \approx 0.1215$



• Trapezoid

  • Base₁ = $1$
  • Base₂ = $1+ 2R\cos \phi - 2R$
  • Height = $R\sin \phi$
  • Area = $\dfrac{(2+ 2R\cos \phi - 2R)\cdot R\sin \phi}{2} = (1 + R\cos\phi - R)\cdot R\sin \phi \approx 0.5839$



• Triangle

  • Base = $1+ 2R\cos \phi - 2R$
  • Height = $r\sin (\frac{\pi}{2}-\phi) = r\cos\phi$
  • Area = $\dfrac{(1+ 2R\cos \phi - 2R)\cdot r\cos\phi}{2} = \left(\dfrac{1}{2}+ R\cos \phi - R\right)\cdot r\cos\phi \approx 0.0218$



• Top, Major Arc Sector

  • Angle = $2\pi - 2\phi$
  • Radius = $r$
  • Area = $\dfrac{2\pi - 2\phi}{2\pi} \cdot \pi r^2 = \pi r^2 - r^2\phi \approx 0.1045$

Answer

$$\boxed{A \approx 0.8317}$$

** Note that as $\theta$ gets smaller, the two large unit arcs get further apart, and the top arc is more likely to be a minor arc than a major arc.

In this scenario, $r = \dfrac{1}{2\phi}$.

The second factor, and thus equation to be solved is now $1 + \dfrac{2\cos \phi - 2}{\phi} - \dfrac{\sin\phi}{\phi} = 0$.

Continuing the idea that $\theta$ gets smaller,
$$\lim_{\phi \to 0} \big(1 + \frac{2\cos \phi - 2}{\phi} - \frac{\sin\phi}{\phi}\big)$$
$$=\lim_{\phi \to 0} 1 + 2\lim_{\phi \to 0} \frac{\cos \phi - 1}{\phi} - \lim_{\phi \to 0} \frac{\sin\phi}{\phi}$$
$$=1 + 0 - 1 = 0$$

$\phi \to 0$ looks like...

Rohan Lewis

2024.11.04

Code can be found here.