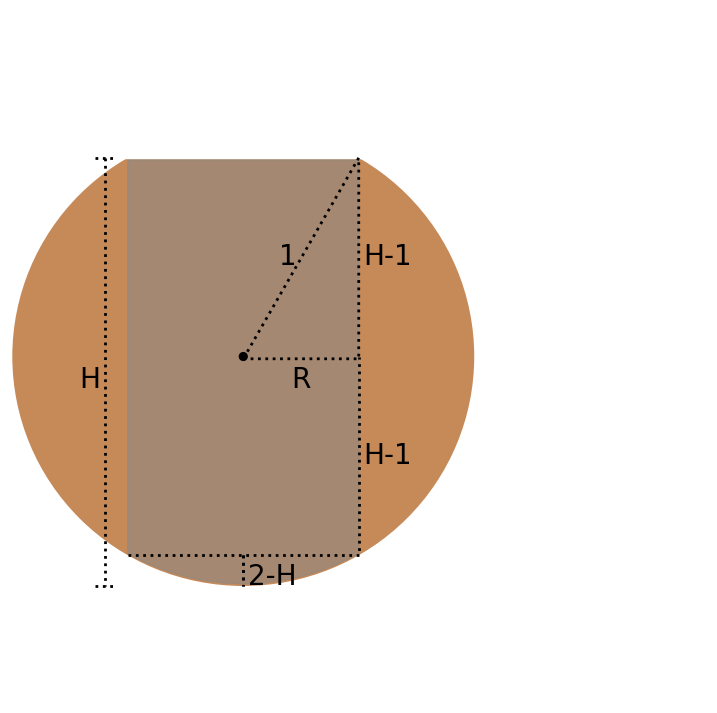
Solution¶

The volume of a cylinder is
$$V = \pi R^2H$$Substituting $R = \sqrt{1-H^2}$ yields:
\begin{align*} V &= \pi \left(\sqrt{1-H^2}\right)^2 H \\ &= \pi \left(H-H^3)\right) \\ \end{align*}In order to maximize volume, set $\dfrac{dV}{dH} = 0$:
\begin{align*} \dfrac{dV}{dH} &= \pi \left(1-3H^2\right) \\ 0 &= 3H^2-1\\ H &=\boxed{\sqrt{\frac{1}{3}}} \end{align*}Substituting into $R = \sqrt{1-H^2}$ yields
$$\boxed{R =\sqrt{\frac{2}{3}}}$$