Can You Beat The Heats?¶

Fiddler¶

From Steven Stern comes a puzzle about speedy runners that you can mull over at a more leisurely pace:

There are 25 sprinters at a meet, and there is a well-defined order from fastest to slowest. That is, the fastest sprinter will always beat the second-fastest, who will in turn always beat the third-fastest, and so on. However, this order is not known to you in advance.

To reveal this order, you can choose any 10 sprinters at a time to run in a heat. For each heat, you only know the ordinal results, so which runner finishes first, second, third, and so on up to 10th. You do not know the specific finishing time for any runner, making it somewhat difficult to compare performances across heats.

Your goal is to determine with absolute certainty which of the 25 sprinters is fastest, which is second-fastest, and which is third-fastest. What is the fewest number of heats needed to guarantee you can identify these three sprinters?

Solution¶

If there were 30 sprinters, 3 heats of 10 and 1 heat of the top three (and a random fourth) would determine the top 3 overall in 4 heats.

Since there are over 2 heats of sprinters, at least 3 heats are required. The third(or fourth) heat must decisively determine the winner. If the first two heats are two independent groups of 10 each, then the third head must be 5 sprinters from the first two heats and 5 who have not ran yet. It would be impossible to eliminate one sprinter from the top 3 in the first two heats with no comparison.

Hence,

  1. Run heat $A$ of 10 sprinters. The top 3, in order, are $A_1$, $A_2$, and $A_3$

  2. Run heat $B$ of 9 new sprinters and $A_2$. There are four possibilities to consider.

    1. The top 3, in order, are $A_2$, $B_2$, and $B_3$. The final heat $C$ should be $A_1$, $A_2$, $B_2$, $A_3$ and the 6 remaining sprinters.
    2. The top 3, in order, are $B_1$, $A_2$, and $B_3$. The final heat $C$ should be $A_1$, $B_1$, $A_2$, the 6 remaining sprinters, and a random sprinter.
    3. The top 3, in order, are $B_1$, $B_2$, and $A_2$. The final heat $C$ should be $A_1$, $B_1$, $B_2$, the 6 remaining sprinters, and a random sprinter.
    4. The top 3, in order, are $B_1$, $B_2$, and $B_3$. The final heat $C$ should be $A_1$, $B_1$, $B_2$, $B_3$ and the 6 remaining sprinters

  3. The top 3 in heat $C$ are the top 3 of the 25.

Answer¶

3 heats is all that is necessary!

Extra Credit¶

At a different meet, suppose there are six sprinters that can race head-to-head. (In other words, there are only two sprinters per heat.) Again, they finish races in a consistent order that is not known to you in advance.

This time, your goal is to determine the entire order, from the fastest to the slowest and everywhere in between. What is the fewest number of head-to-head races needed to guarantee you can identify this ordering?

Solution¶

I will look at fewer sprinters.

1 Sprinter¶

0 races are required to determine the ordering

2 Sprinters¶

1 race is required to determine the ordering

3 Sprinters¶

WLOG, consider an additional sprinter joining late after the ordering of 2 sprinters is determined. The worse case scenario is that the new sprinter has to run against each individually.

3 races are required to determine the ordering.

...¶

$n$ Sprinters¶

Consider an additional sprinter joining late after the ordering of $n-1$ sprinters is determined.

Using a binary search algorithm, the $n^\text{th}$ sprinter requires at most $\lceil\log(n)\rceil$ races.

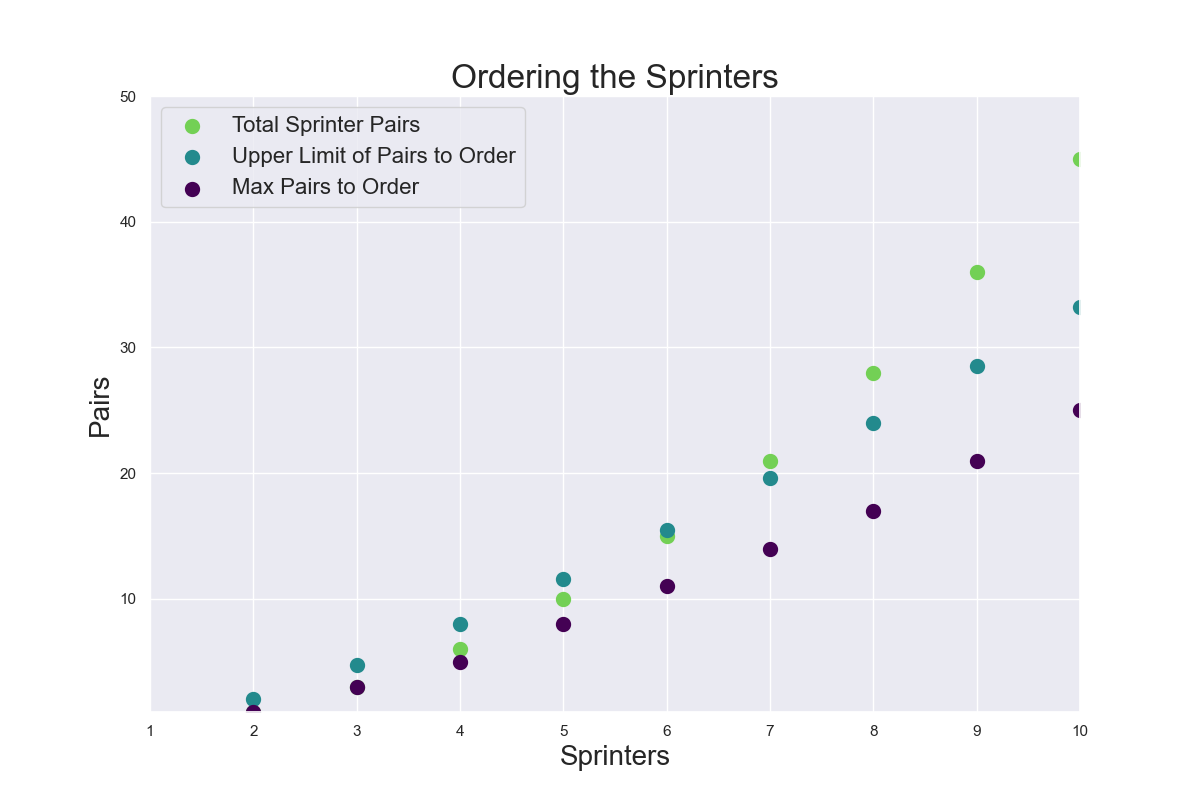
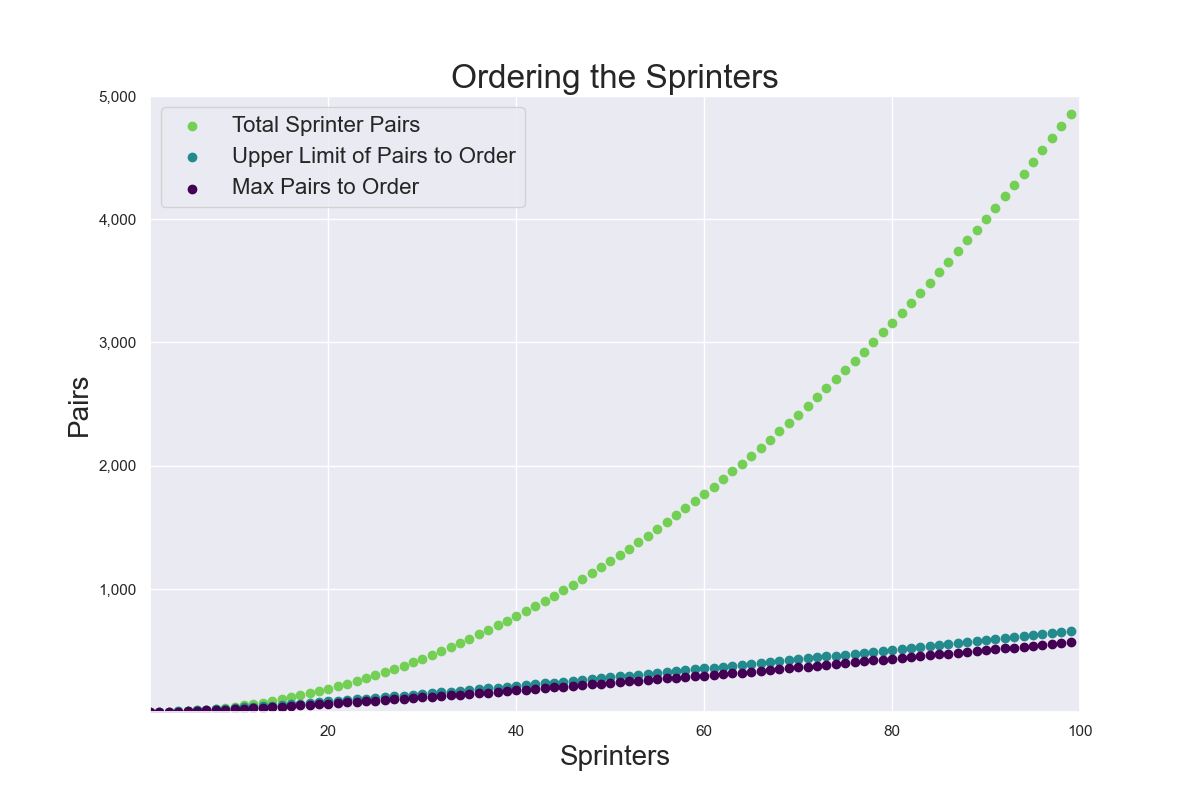
The number of head-to-head races is:

$M(n) = \sum\limits_{i=1}^n \lceil\log_2(i)\rceil$

Answer¶

$$M(6) = \lceil\log_2(1)\rceil + \lceil\log_2(2)\rceil + \lceil\log_2(3)\rceil + \lceil\log_2(4)\rceil + \lceil\log_2(5)\rceil + \lceil\log_2(6)\rceil$$$$= 0 + 1 + 2 + 2 + 3 + 3 = 11$$

The total number of head-to-head races for $n$ sprinters is:
$$T(n) = \dfrac{n(n-1)}{2}$$
An upper limit approximation for $M(n)$ is
$$U(n) = n \cdot \log_2 n$$

Some plots to go with...

Rohan Lewis¶

2024.05.05¶

Code can be found here.