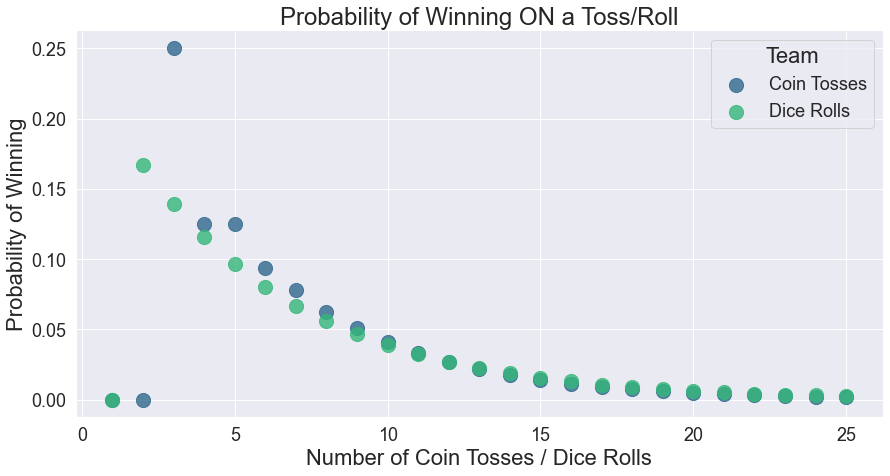
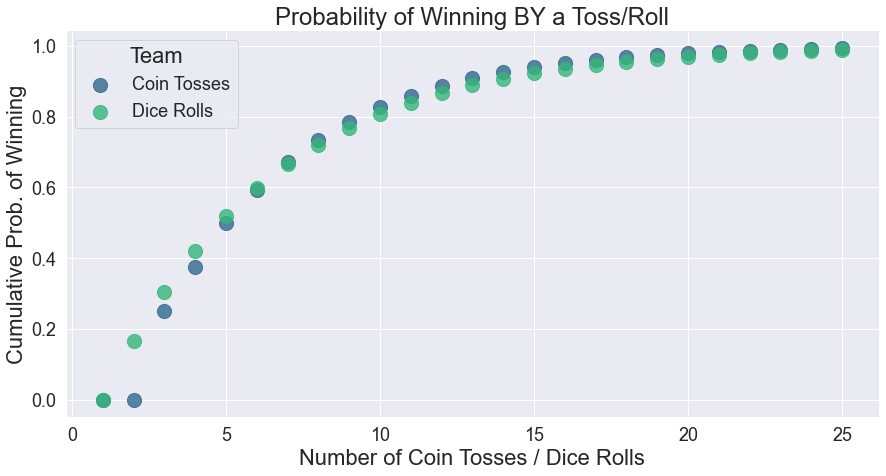
3. Average Number of Flips¶
The following Markov Chain represents achieving a coin being the same for three consecutive flips.
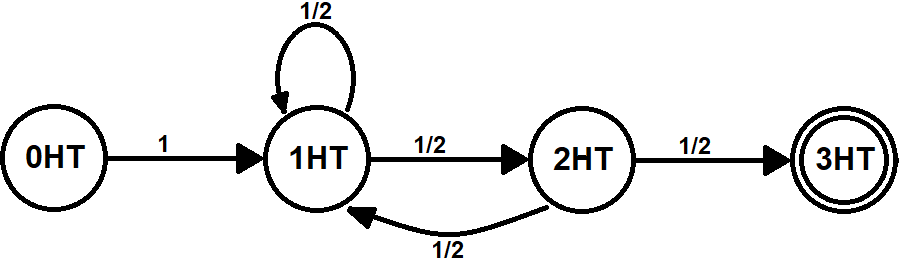
- The first flip does not matter.
- As long as the next flip is the same as the previous flip, it stays on the center branch.
- If a flip is different from the previous flip, it goes to 1HT.
The average number of flips to get three consecutive can be calculated as:
$$EV_F = 1\cdot\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot 3 + \dfrac{1}{2}\cdot(1 + EV_F) + \dfrac{1}{4}\cdot(2 + EV_F)$$
$$EV_F = \dfrac{3}{4} + \dfrac{1}{2}+ \dfrac{1}{2}EV_F + \dfrac{1}{2} + \dfrac{1}{4}EV_F$$
$$\dfrac{1}{4}EV_F = \dfrac{7}{4}$$