From Chris Gerig comes a variant of the famed Monty Hall problem:
In a game show, there are three identical doors arranged in a row from left to right. The host of the show, “Monty,” chooses one of the doors and places a prize of \$100 dollars behind it. There is no prize behind the other two doors. You are not present when Monty chooses the door and places the money behind it, so you cannot say for certain which door the prize is behind.
You are then brought to the stage and must select one of the three doors to open. If the prize money is behind it, then you win! But if you guess incorrectly, all is not lost. You can pay \$80 to pick a second door. Before you make that second selection, however, Monty will give you a hint, telling you whether the prize is behind a door that’s to the left or to the right of your first choice. (Note that this hint is only helpful when you previously selected the middle door.) If the prize isn’t behind that second door, you can pay another \$80 to try a third time.
Assume that both you and Monty play with optimal strategies — you to maximize your expected net earnings (prize winnings minus payments for hints), and Monty to minimize the same. How much net earnings can you expect to make on average?
Extra credit: Suppose Monty has you pay \$80 up front before selecting your first door, and each subsequent selection (if you choose to make it) continues to cost \$80. If the prize money remains \$100, this game isn’t worth playing. How much should the prize money be to make the game worthwhile?
This is a sequential, zero-sum game.
Monty has three initial strategies, that is, placing the cash behind the Left, Center, or Right doors.
You in response have three response strategies, that is, choosing the Left, Center, or Right doors.
The following table summarizes all strategies, outcomes, and payoffs. Since this is a zero-sum game, the values are Your earnings and Monty's losses.
| Monty's Choice | ||||
|---|---|---|---|---|
| Left | Center | Right | ||
| Your Choice | Left | \$100 | \$0 | \$0 |
| Center | \$20 | \$100 | \$20 | |
| Right | \$0 | \$0 | \$100 | |
Left and Right can be interchanged for you and Monty without changing the outcome.
Therefore:
The following table provides the expected values:
| Monty's Choice | ||||
|---|---|---|---|---|
| Left | Center | Right | ||
| Your Choice | Left | $100my$ | $0(1-2m)y$ | $0my$ |
| Center | $20m(1-2y)$ | $100(1-2m)(1-2y)$ | $20m(1-2y)$ | |
| Right | $0my$ | $0(1-2m)y$ | $100my$ | |
| Monty's Choice | ||||
|---|---|---|---|---|
| Left | Center | Right | ||
| Your Choice | Left | $100my$ | $0$ | $0$ |
| Center | $20m-40my$ | $400my - 200m - 200y + 100$ | $20m-40my$ | |
| Right | $0$ | $0$ | $100my$ | |
$$ = 520my - 160m - 200y +100$$
This represents the average net earnings to you (loss to Monty) for each play of this game.
The optimal solution is the Nash Equilibrium, that is, the strategies chosen where neither player gains by deviating.
For some value you $m$, you will always receive $-160m + 100$. However, $520my-200y$ should remain unchanged. This occurs when $m = \frac{5}{13}$.
For some value you $y$, you will always receive $-200y + 100$. However, $520my-160m$ should remain unchanged. This occurs when $y = \frac{4}{13}$.
The payoff to you is thus:
$$520\left(\dfrac{5}{13}\right)\left(\dfrac{4}{13}\right) - 160\left(\dfrac{5}{13}\right) - 200\left(\dfrac{4}{13}\right) +100 = \frac{6500}{169} \approx \text{\$} 38.46$$Monty will choose Left, Center, Right with probabilities $\left(\dfrac{5}{13}, \dfrac{3}{13}, \dfrac{5}{13}\right)$.
You will choose Left, Center, Right with probabilities $\left(\dfrac{4}{13}, \dfrac{5}{13}, \dfrac{4}{13}\right)$.
Your expected net earnings each round \$38.46.
Note that every point along the vertical line representing Monty's $\dfrac{5}{13}$ as well as the horizontal line representing Your $\dfrac{4}{13}$ yields \$38.46.
Let $E$ be the earnings necessary to make the game worthwile.
This modifies the earnings table to:
| Monty's Choice | ||||
|---|---|---|---|---|
| Left | Center | Right | ||
| Your Choice | Left | $Emy$ | $0(1-2m)y$ | $0my$ |
| Center | $(E-80)m(1-2y)$ | $E(1-2m)(1-2y)$ | $(E-80)m(1-2y)$ | |
| Right | $0my$ | $0(1-2m)y$ | $Emy$ | |
| Monty's Choice | ||||
|---|---|---|---|---|
| Left | Center | Right | ||
| Your Choice | Left | $Emy$ | $0$ | $0$ |
| Center | $Em - 80m - 2Emy + 160my$ | $4Emy - 2Em - 2Ey + E$ | $Em - 80m - 2Emy + 160my$ | |
| Right | $0$ | $0$ | $Emy$ | |
Average Net Earnings:
$$ = 320my+2Emy-2Ey-160m+E$$
$$ = (160+E)2my-2Ey-160m+E$$
Note that \$80 is subtracted from the entire expected earnings, as that is what you pay to initially choose.
Thus the average net earnings to you (loss to Monty) for each play of this game is now $(160+E)2my-2Ey-160m+E-80$
Similar to above, we will determine the probabilities for the Nash Equilibrium, but then use them to find the minimum value of $E$ to make the earnings positive for you.
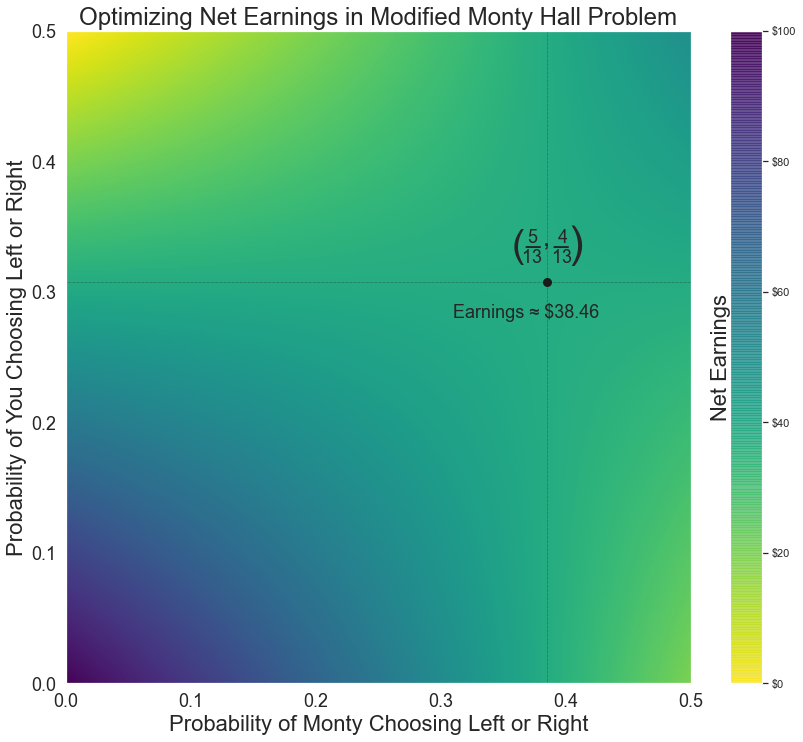
For some value you $m$, you will always receive $-160m + E - 80$. However, $320my+2Emy-2Ey$ should remain unchanged. This occurs when $m = \frac{E}{160+E}$.
For some value you $y$, you will always receive $-2Ey + E - 80$. However, $320my+2Emy-160m$ should remain unchanged. This occurs when $y = \frac{80}{160+E}$.
Substituting the above values of $m$ and $y$,
$$0 < \left(160+E\right)\cdot 2 \cdot \left(\dfrac{E}{160+E}\cdot\dfrac{80}{160+E}\right) - \left(2E\cdot\dfrac{80}{160+E}\right) - \left(160\cdot\dfrac{E}{160+E}\right) + \left(E-80\right)$$
$$0 < \dfrac{160E}{160+E} - \dfrac{160E}{160+E} - \dfrac{160E}{160+E} + \left(E-80\right)$$
$$0 < -160E +\left(E-80\right)(E+160)$$
$$0 < -160E + E^2 +160E - 12800$$
$$12800 < E^2$$
$$E > \sqrt{12800} \approx 113.14$$
There must be at least \$113.14 prize money to make the game worthwhile to you.