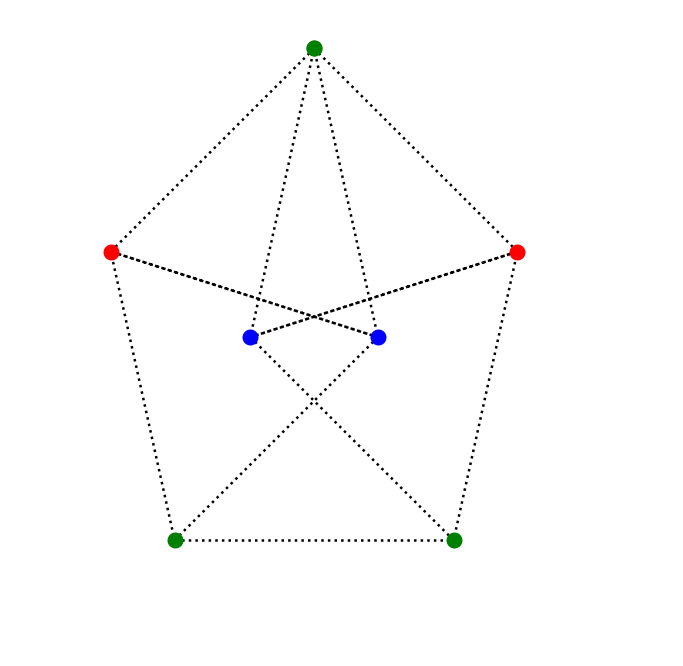
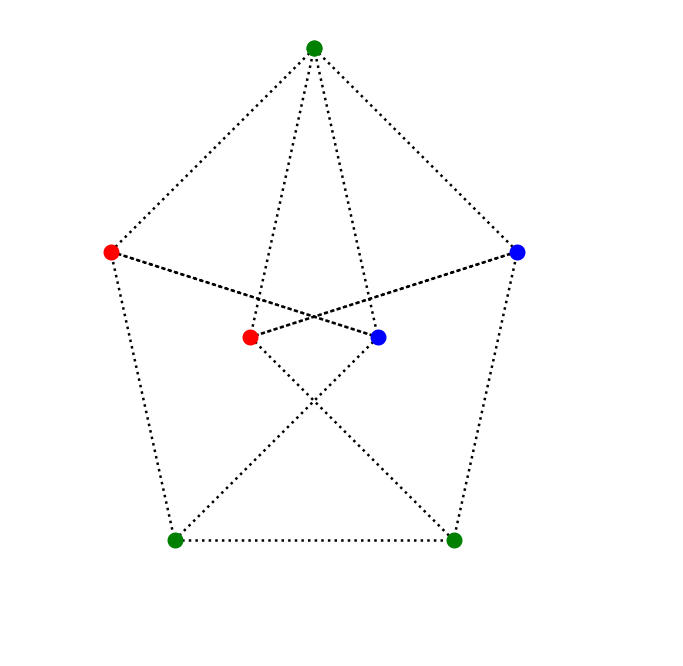
Solution¶
Consider two equilateral triangles of side length 1, sharing two vertices and an edge, such that vertices on the same edge are of different colors.
WLOG they will always look like this, the points $\sqrt{3}$ units apart must be the same color.
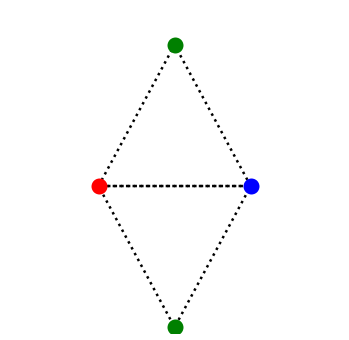
Consider the following equilateral triangle.
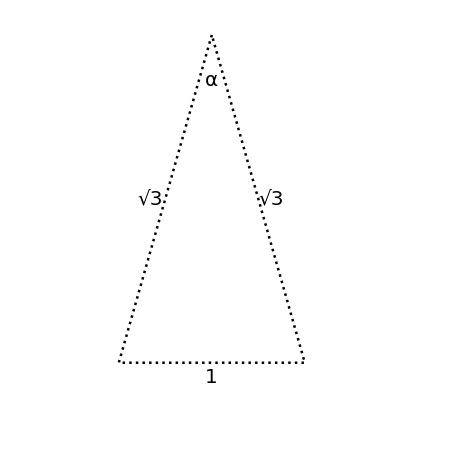
$α = 2 \cdot \sin ^{-1} \left(\dfrac{\dfrac{1}{2}}{\sqrt{3}}\right) \approx 33.5573^{\circ}$