Can You 'Waffle' Your Way To A Proof?¶
Riddler Classic¶
As you may have heard, two high school students from St. Mary’s Academy in New Orleans, Louisiana — Ne’Kiya Jackson and Calcea Johnson — recently discovered a novel proof of the Pythagorean Theorem.
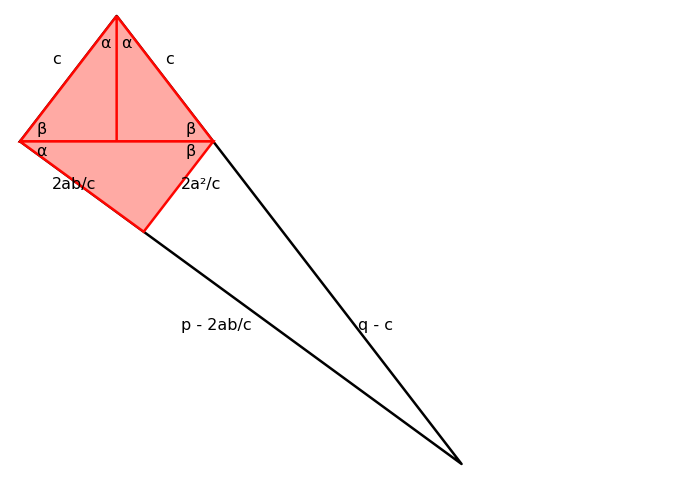
Their proof applied the law of sines (which itself can be derived from equivalent expressions for a triangle’s area and has no dependency on the Pythagorean theorem, thereby avoiding any circular logic) to the construction below:

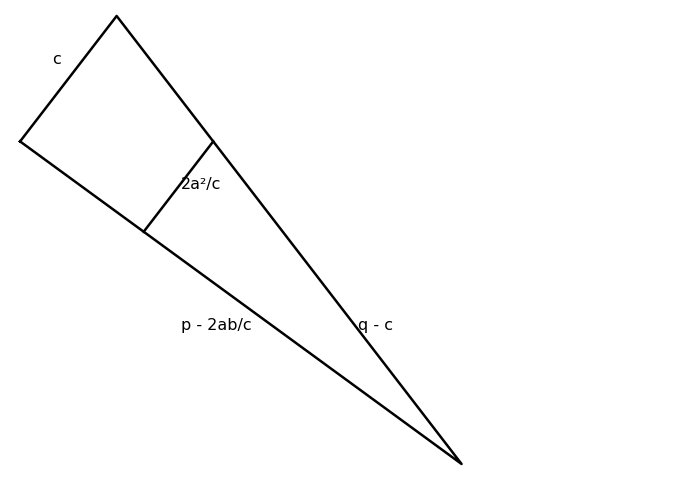
Atop the figure are two reflected right triangles with legs a and b (with a < b) and hypotenuse c. Below these triangles are what the students called a “waffle cone” shape, formed between the extensions of one of the top triangle’s hypotenuse and a line that’s perpendicular to the other hypotenuse.
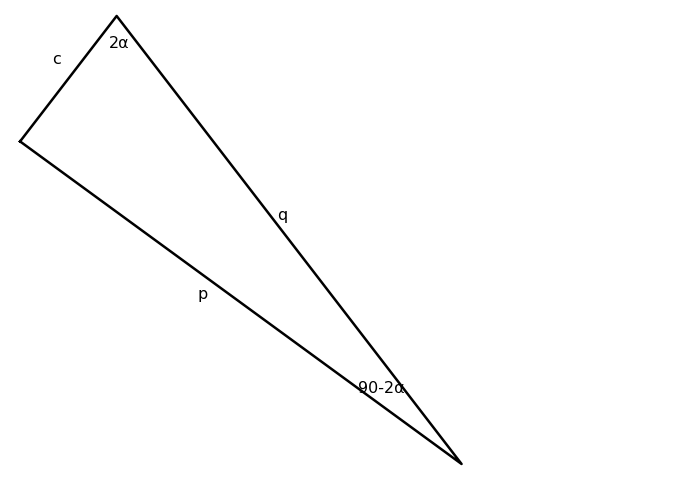
In their proof, they compute distances p and q, where p extends from the leftmost vertex of the two triangles to the intersection of the lines, and q extends from the topmost vertex of the two triangles to the same intersection.
Your challenge is to determine expressions for p and q in terms of a, b and c. However, in doing so, you absolutely cannot use the Pythagorean theorem in any of its forms (e.g., the so-called “distance formula,” etc.). After all, solving for p and q is a key step toward proving the Pythagorean theorem.
Extra credit: Once you’ve determined p and q, try completing a proof of the Pythagorean theorem that makes use of them. Remember, the students used the law of sines at one point.