Can You Create All The Sequences?

Riddler Express

From composer Grant Harville comes a musical mystery:

Grant is writing a musical composition. At one point in the piece, there’s an improvisational passage where musicians are instructed to repeatedly play a sequence of eight notes, which we can label as 1 through 8. The shortest such sequence is 12345678.

However, musicians can also revert to previous notes, replaying certain subsequences for additional flair. More specifically:

1. They must always play the next note (i.e., adding 1 to the previous note), unless they revert to a previous note.
2. At no point can they play the same note twice in a row.
3. Notes 1 and 8 — that is, the first and last notes — can be played only once.
4. They can only revert to a given note at most once.
5. Once they have reverted to a specific note, they cannot then revert to an earlier note in the sequence.

That’s a whole bunch of rules! To make this clearer, it may be helpful to see some examples. The following are examples of valid sequences:

• 12345678 (This is the shortest sequence.)
• 1234567-234567-34567-4567-567-678 (This is the longest sequence.)
• 1234-234567-678
• 1234567-345-4567-5678
• 123-234567-3456-45678

Meanwhile, here are examples of invalid sequences, for various reasons:

• 1245678 (This skips the 3.)
• 12437568 (Some notes are out of order.)
• 12345-34678 (This skips a note within a reversion, even though that note occurs earlier.)
• 1234-3456-345678 (This reverts to the same note twice.)
• 12345-456-2345678 (This reverts to an earlier note after reverting to a later one.)
• 12345-567-678 (This repeats a note twice in a row.)
• 123-1234567-5678 (This repeats note 1.)
• 1234-23456-5678-78 (This repeats note 8.)

How many different sequences of the eight notes are possible under these conditions?

Solution

I wrote code:

1. Notes = 1, 2, 3:
   • Notes = 1, sequence = 1.
   • Notes = 2, sequence = 12.
   • Notes = 3, sequence = 123.
2. For Notes ≥ 4 :
   1. Begin sequence with 12.
   2. Append the next note.
   3. If the most recent appended number is the last note, the sequence ends.
   4. Branch two possibile child sequences:
      1. Play Next Note - go to B.
      2. Start a Reversion:
         1. Begin with any note that is :
            • Greater than the first note of the initial sequence or previous reversion.
            • Less than or equal to the highest value note that has been played thus far.
            • Not equal to the most recent note played.
         2. Append the next note.
         3. If the most recent appended number is the last note, the sequence ends.
         4. Branch two possibile child sequences:
            1. Play Next Note - go to ii.
            2. Start a new Reversion - go to b.

I collected all sequences from C and iii for 1 to 10 notes.

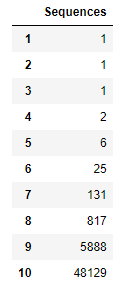
Some subtle differences in the sequences.

123456-23678 is an invalid sequence, but 123456-23-678 is valid.

123456-2345678, 123456-234-5678, 123456-23-45-678 are different sequences using reversions, but the same by note sequence.

Answer

817 sequences for 8 notes if defined by note order.

1939 sequences for 8 notes if defined by reversions.

Rohan Lewis

2023.03.20

Code can be found here.