Can You Balance The Target?¶
Riddler Express¶
From Kyle Willstatter comes a puzzle that’s right on target:
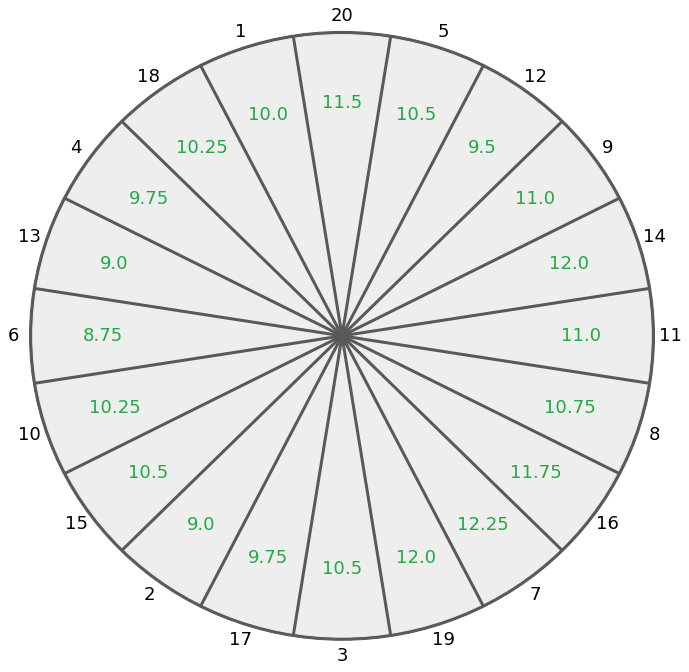
You’re playing darts and trying to maximize the number of points you earn with each throw. You are deciding which sector to aim for. Your dart has a 50 percent chance of landing in that sector and a 25 percent chance of landing in one of the two neighboring sectors. Reading clockwise, the sectors are worth 20, 1, 18, 4, 13, 6, 10, 15, 2, 17, 3, 19, 7, 16, 8, 11, 14, 9, 12 and 5 points, as shown below. (For the purposes of this puzzle, don’t worry about the bullseye, the outer ring that’s worth double or the inner ring that’s worth triple.)

Which sector should you aim for to maximize your expected score?
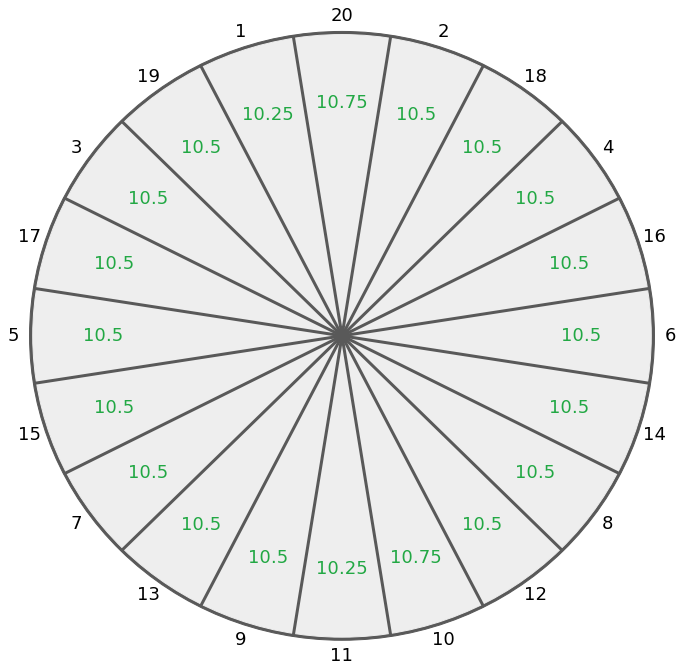
Extra credit: How would you “fairly” (by some definition of fair for you to define) assign the point values around a dartboard? Explain your thinking.