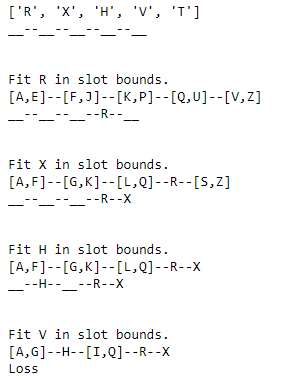Can You Defeat The TikTok Meme?

Riddler Classic

From Angela Zhou comes a challenging meme analysis:

The #blindletterchallenge has recently taken TikTok by storm. In this challenge, you are presented with five letters, one at a time. Letters are picked randomly, but you can assume that no two letters are the same (i.e., letters are picked without replacement). As each letter is presented, you must identify which of five slots you will place it. The goal is for the letters in all five slots to be in alphabetical order at the end.

For example, consider an attempt at the challenge by Michael DiCostanzo. The first letter is X. Since this occurs relatively late in the alphabet, he puts this in the fifth slot. The second letter is U. He puts that in the fourth slot, since it also comes relatively late (and the fifth slot is already occupied). Next, the third letter is E. He takes a gamble, and places E in the first slot. The fourth letter is D. Since D comes before E alphabetically, but no slots prior to E are now available, Michael loses this attempt.

If you play with an optimal strategy, always placing letters in slots to maximize your chances of victory, what is your probability of winning?

Solution

Consider placing a letter in the 1^st slot vs 2^nd slot.

• Let the letter be the $k$^th letter from $1$^st to $l$^th
• There are $l-1$ letters remaining for $s-1$ slots.
• If placing in $1$^st slot:
  • The $1$^st to $(k-1)$^st are no longer viable letters.
  • The $(k+1)$^st to $l$^th letters are to be placed in the $2$^nd to $s$^th slots.
• If placing in $2$^nd slot:
  • The $1$^st to $(k-1)$^st letters are to be placed in the $1$^st slot.
  • The $(k+1)$^st to $l$^th letters are to be placed in the $3$^rd to $s$^th slots.

Let us find the value of $k$ for which placing in $1$^st slot is better than placing in $2$^nd slot:

$${{l-(k+1)} \choose {s-1}} > {{k-1} \choose {1}} \cdot {{l-(k+1)} \choose {s-2}}$$
$$\dfrac{\big(l-(k+1)\big)!}{\big(l-(k+1)-(s-1)\big)! \cdot (s-1)!} > \dfrac{(k-1)\cdot\big(l-(k+1)\big)!}{\big(l-(k+1)-(s-2)\big)! \cdot (s-2)!}$$
$$\dfrac{1}{s-1} > \dfrac{k-1}{l-(k+1)-(s-2)}$$
$$l-k-1-s+2 > k(s-1)-1(s-1)$$
$$l-s+1 +1(s-1) > k(s-1)+k$$
$$l > ks$$
$$k < \dfrac{l}{s}$$

Let us find the value of $k$ for which placing in $2$^nd slot is better than placing in $3$^rd slot:

$${{k-1} \choose {1}} \cdot {{l-(k+1)} \choose {s-2}} > {{k-1} \choose {2}} \cdot {{l-(k+1)} \choose {s-3}}$$
$$\dfrac{(k-1)\cdot\big(l-(k+1)\big)!}{\big(l-(k+1)-(s-2)\big)! \cdot (s-2)!} > \dfrac{(k-1)\cdot(k-2)\cdot\big(l-(k+1)\big)!}{2\big(l-(k+1)-(s-3)\big)! \cdot (s-3)!}$$
$$\dfrac{1}{s-2} > \dfrac{k-2}{2-(2k+2)-(2s-6)}$$
$$2l-2k-2-2s+6 > k(s-2)-2(s-2)$$
$$2l-2s+4 + 2(s-2) > k(s-2)+2k$$
$$2l > ks$$
$$k < \dfrac{2l}{s}$$

Note that no more comparisons need to be made.

Placing in $(s-1)$^st slot is better than placing in $(s-2)$^nd is equivalent to placing in $2$^nd slot is better than placing in $3$^rd.

Placing in $s$^th(last) slot is better than placing in $(s-1)$^st is equivalent to placing in $1$^st slot is better than placing in $2$^nd.

It seems that setting ranges of equal letter lengths for consecutive slots is the way to go.

My code generated all $26 \choose 5$ sequences of five unique letters. For each sequence:

1. Start with a blank set of ranges for each slot.
2. Divide number of letters to be filled in consecutive slots by number of consecutive slots. Consecutive slots may be from 1 - 5, and there may be more 1-3 of them.
3. Fit current letter in slot range.
• If it cannot be fit, return Loss.
• If it can be fit, replace range with letter.
• If it is the fifth letter, return Win.
• If not, keep all other placed letters, clear all ranges. Repeat steps 2 - 3.

Here is an example:

Answer

Running for all ${26 \choose 5} = 7,893,600$ letter sequences yielded $1,948,258$ wins and $5,945,342$ losses.

$$\dfrac{1948258}{7893600} \approx 0.2468149$$

.

Rohan Lewis

2023.02.01

Code can be found here.