Solution¶
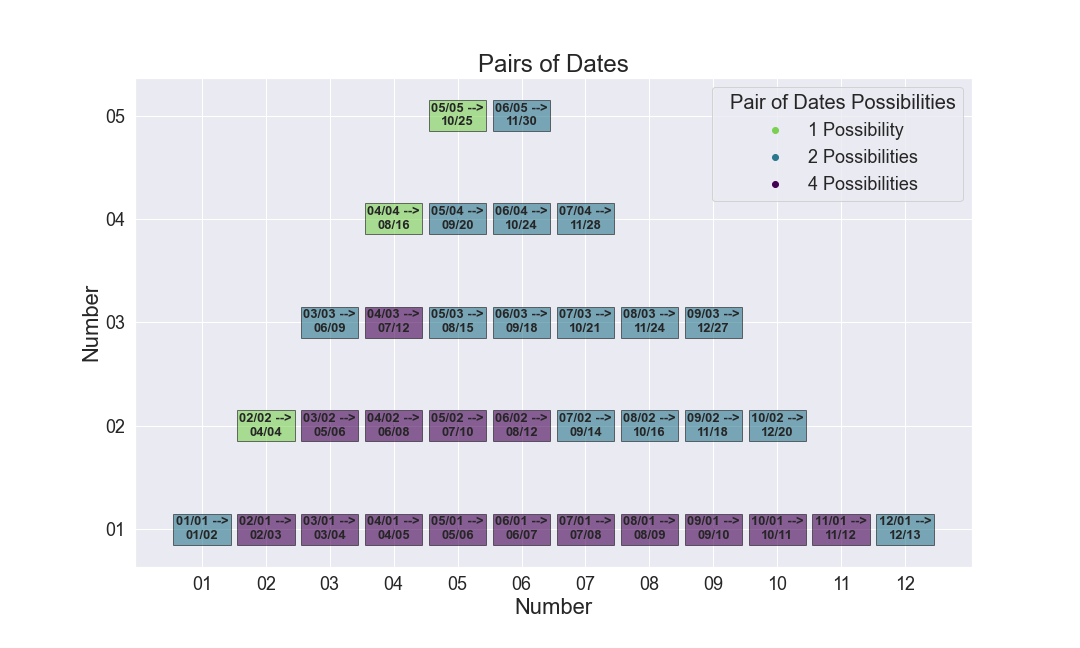
There are two dates. Lets loosely define them as the Original and Computed.
Original Date¶
The maximum either of the numbers in the Original Date can be is 12. If there were any number greater than 12, then both the product and sum of the Computed Date would be greater than 13.
The two numbers are interchangeable unless they are equal. 01/01 is an example.
Computed Date¶
The maximum of one number in the Computed Date is 31. The maximum of the other number in the Computed Date is 12.
The two numbers are interchangeable if they are both 12 or less. However they are not interchangeable in the special case of 04/04.
Impossible Dates¶
Even with correct calculations, the dates could possibly not exist in the calendar.
Fortunately these never occured. It is not possible to get a product of 29 or 30 with a sum of 2. A product of 31 also never occurs.