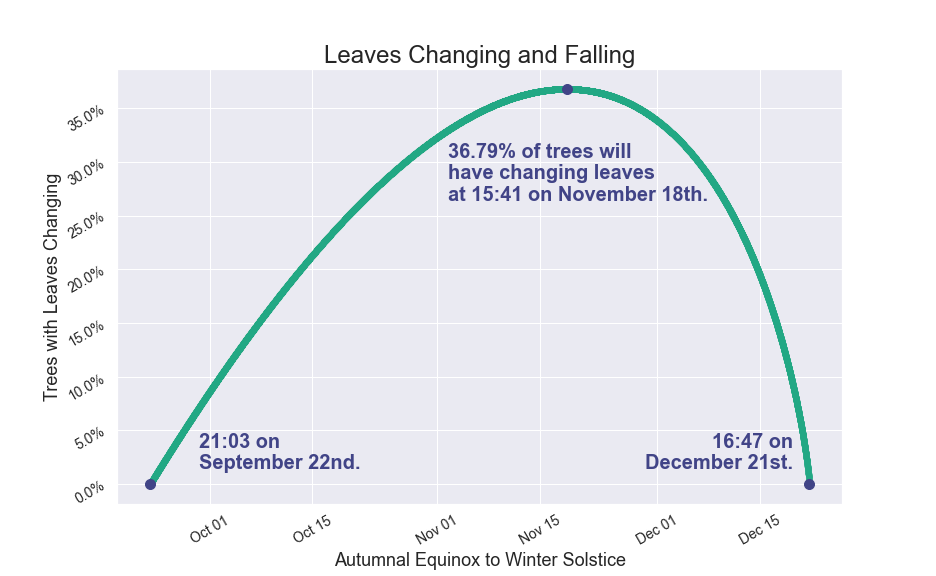
Answer¶
Substituting $t$ into $f(t) = (t-1) \ln (1-t)$,
$$f\left(1 - \dfrac{1}{e}\right) = \left(\left(1 - \dfrac{1}{e}\right) - 1\right) \ln \left(1-\left(1 - \dfrac{1}{e}\right)\right)$$
$$f\left(1 - \dfrac{1}{e}\right) = \left(- \dfrac{1}{e}\right) \ln \left(\dfrac{1}{e}\right) = \dfrac{1}{e} \approx 36.79\%$$