Can You Knock Down The Last Bowling Pin?

Riddler Classic

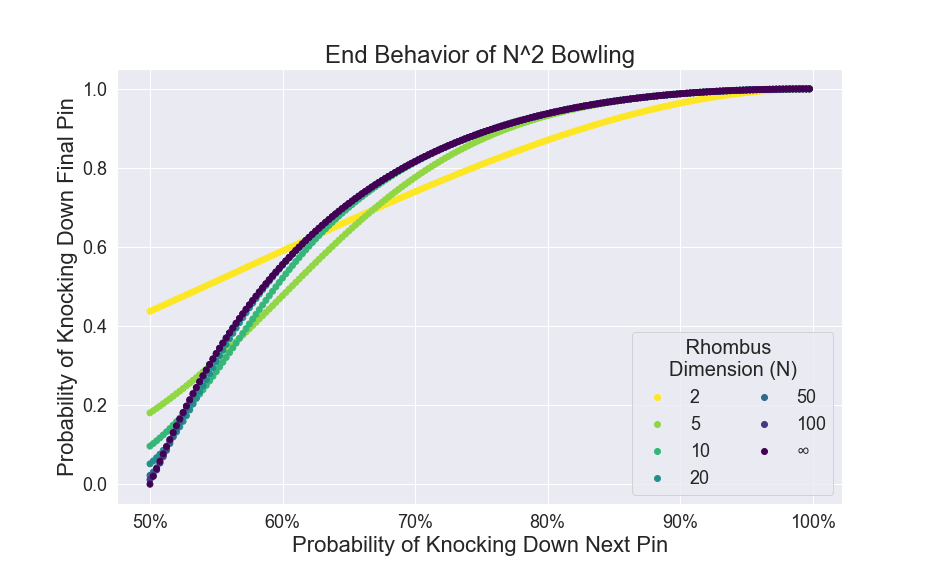
Magritte the bowler is back! This time, he is competing head-to-head against fellow bowler Fosse. However, rather than knocking down 10 pins arranged in a triangular formation, they are trying to knock down N² pins (where N is some very, very large number) arranged in a rhombus, as shown below:

When Magritte rolls, he always knocks down the topmost pin. Then, if any pin gets knocked down, it has a 50 percent chance of knocking down either of the two pins directly behind it, independently of each other. (If there is only one pin directly behind it, then it too has a 50 percent chance of being knocked over.)

Fosse is a stronger bowler than Magritte. Like Magritte, she always knocks down the topmost pin. But each pin that’s knocked down then has a 70 percent chance (rather than Magritte’s 50 percent) of knocking down any of the pins directly behind it.

What are Magritte’s and Fosse’s respective probabilities of knocking down the bottommost pin in the rhombus formation?

Solution

Let $N$ be the dimension of the rhombus, and $p$ be the probability that a pin knocked down knocks down the next pin.

I ran code to determine successive probabilities:

• The first row is $0-1-0$.
• Using inclusion-exclusion, the probability each pin in the next N-1 rows is computed by $pP_l + pP_r - p^2P_lP_r$, where $P_l$ and $P_r$ represent the respective probabilities that the two pins directly above have been knocked over. A single 0 is appended to the beginning and end of the row, to increase the number of pins by 1 in the next row.
• Once the Nth row is computed, the same procedure is applied for N-1 more rows. 0's are not appended to the beginning and end of the row, to decrease the number of pins by 1 in the next row.
• The probability of the pin in the last (bottommost) row is saved.

For each rhombus dimension N = 2, 5, 10, 20, 50, and 100, I ran the code for probabilities from 50 - 100%.

The ∞ represents evaluating the expression $\dfrac{2p-1}{p^2} = 1 - \left(1-\dfrac{1}{p}\right)^2$. This seems to be the value that larger rhombi approach.

Answer

Magritte's probability ≈ 0. Fosse's probabilty is ≈ $\dfrac{40}{49}$.

Rohan Lewis

2022.08.05

Code can be found here.