Solution¶
The following diagram illustrates the initial scenario.
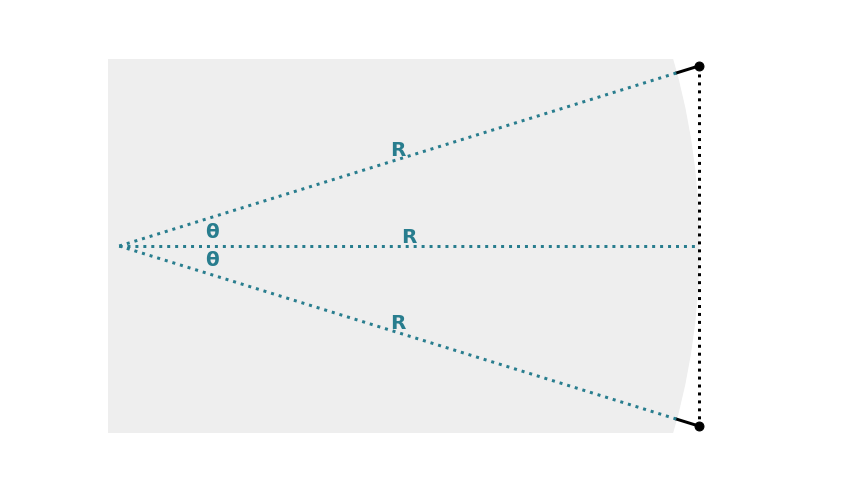
From this,
$$ \cos θ = \dfrac{R}{R+100}$$
As the Royal Astronomer of Planet Xiddler, you wake up from a dream in which you measured the planet’s radius using a satellite. “How silly!” you think to yourself. “Satellites haven’t even been invented yet!” And so you and another astronomer set out to investigate the curvature of the planet.
The two of you climb two of the tallest towers on the planet, which happen to be in neighboring cities. You both travel 100 meters up each tower on a clear day. Due to the curvature of the planet, you can barely make each other out.
Next, your friend returns to the ground floor of their tower. How high up your tower must you be so that you can just barely make out your friend again?
The following diagram illustrates the initial scenario.

From this,
$$ \cos θ = \dfrac{R}{R+100}$$
The following diagram illustrates the second scenario.
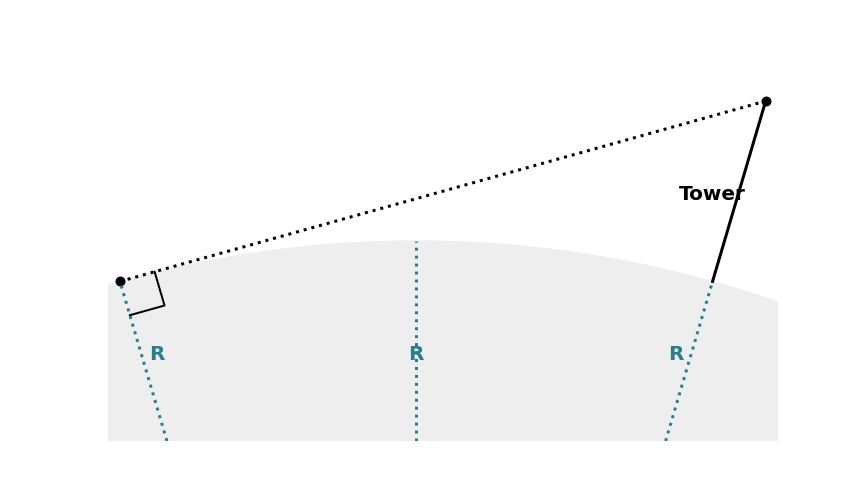
Considering the central angle,
$$ \cos 2θ = \dfrac{R}{R+T}$$
Where $T$ is the tower height.
Using the identity $\cos 2θ = 2\cos^2θ -1$,
$$\dfrac{R}{R+T} = 2\left(\dfrac{R}{R+100}\right)^2 - 1$$
$$R(R+100)^2 = 2R^2(R+T) - (R+100)^2(R+T)$$
$$\dfrac{R(R+100)^2}{2R^2 - (R+100)^2} = R+T$$
The final tower height to see your friend depends on the radius of Xiddler (or the central angle between the two original 100m towers).

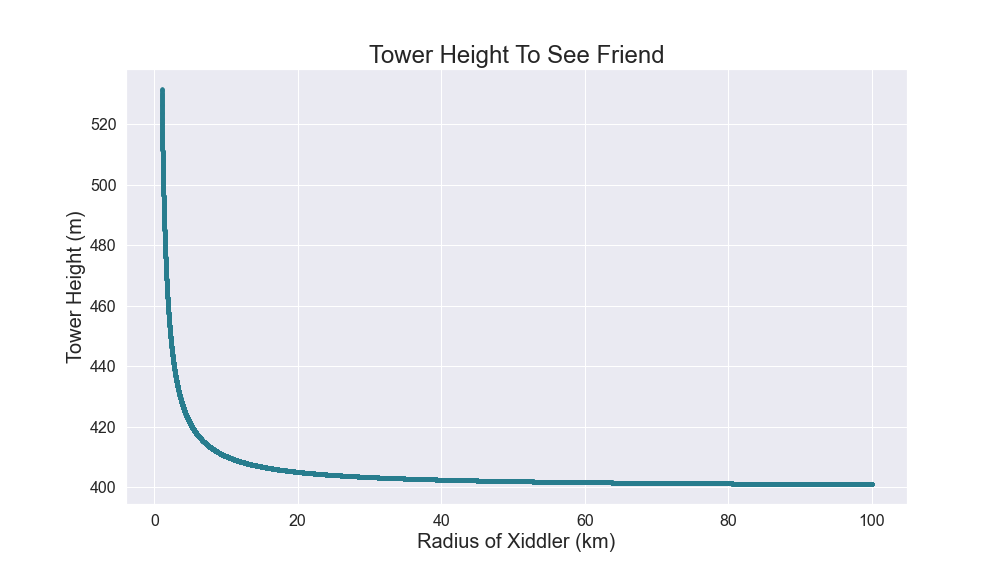
Given a planet of reasonable size, with the two cities being < 5° apart, the final tower will be ≈ 400m.