From Quoc Tran comes a caprine conundrum:
A goat tower has 10 floors, each of which can accommodate a single goat. Ten goats approach the tower, and each goat has its own (random) preference of floor. Multiple goats can prefer the same floor.
One by one, each goat walks up the tower to its preferred room. If the floor is empty, the goat will make itself at home. But if the floor is already occupied by another goat, then it will keep going up until it finds the next empty floor, which it will occupy. But if it does not find any empty floors, the goat will be stuck on the roof of the tower.
What is the probability that all 10 goats will have their own floor, meaning no goat is left stranded on the roof of the tower?
If all goats have their own floor, then for any outcome of goat preferences, each goat's preference will be less than or equal to their respective floor.
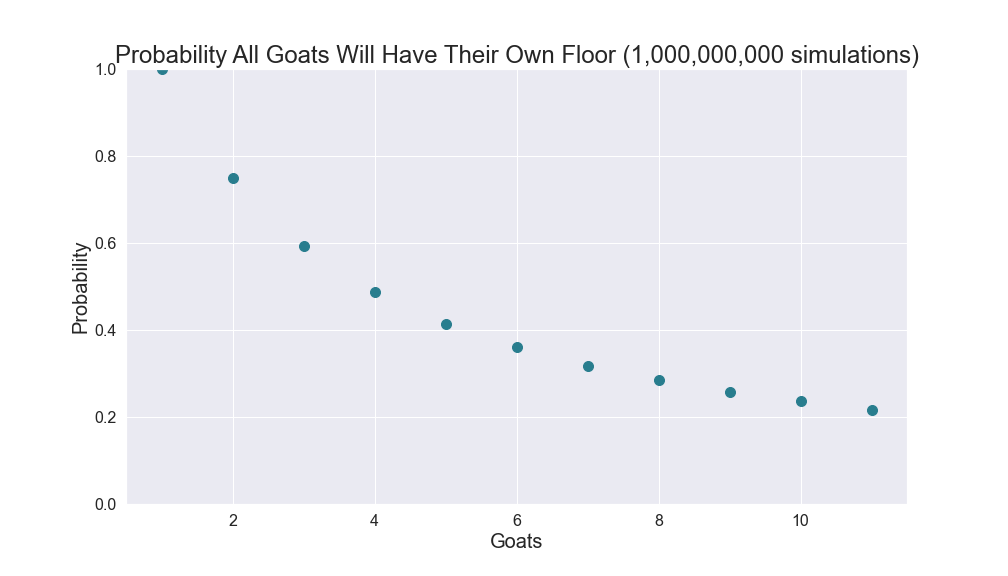
Given g, the number of goats, I wrote some code:

I do not know why, but the probability seems to be the same as $\dfrac{(g+1)^{g-1}}{g^g}$.
| Goats | Simulation of 1,000,000,000 | $\dfrac{(g+1)^{g-1}}{g^g}$ |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0.750004596 | 0.75 |
| 3 | 0.592558973 | 0.59259 |
| 4 | 0.488287741 | 0.48828 |
| 5 | 0.414732100 | 0.41472 |
| 6 | 0.360210095 | 0.36023 |
| 7 | 0.318294739 | 0.31831 |
| 8 | 0.285087681 | 0.28509 |
| 9 | 0.258127130 | 0.25812 |
| 10 | 0.235781540 | 0.23579 |
| 11 | 0.217040838 | 0.21702 |