This expression is the same as the beginning if b = 19. It also occured to me that the opposite, 11 red balls and 8 white balls remain in the urn.
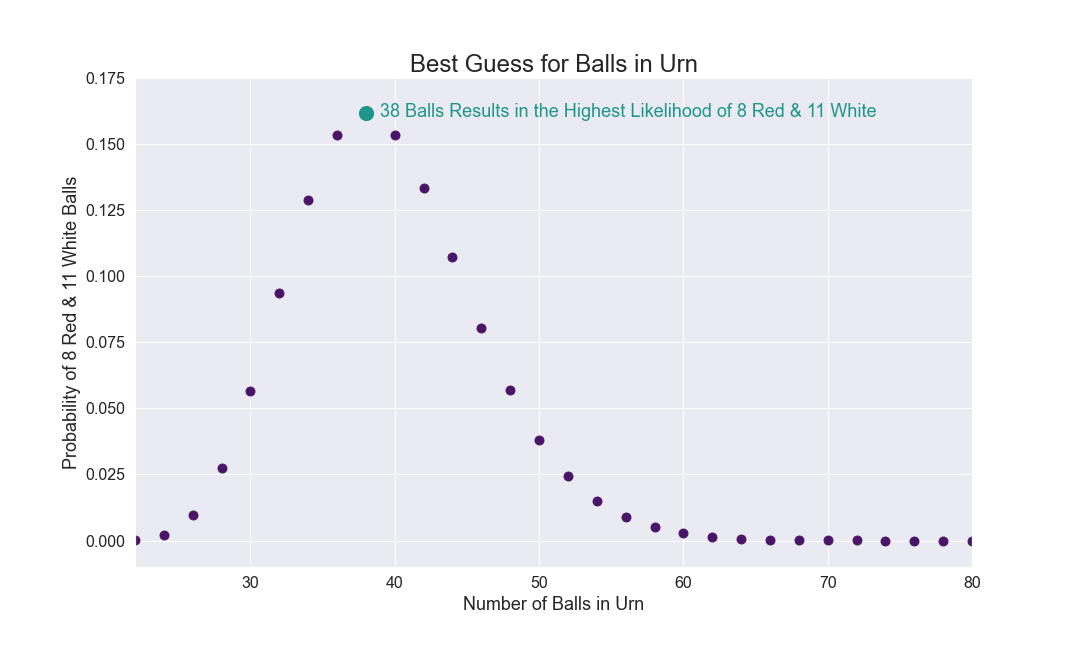
Not convinced that this is the answer, I graphed the probabilities from 11 to 40.
This week’s Classic may seem nonsensical at first. But surely there’s more to it …
You have an urn with an equal number of red balls and white balls, but you have no information about what that number might be. You draw 19 balls at random, without replacement, and you get eight red balls and 11 white balls. What is your best guess for the original number of balls (red and white) in the urn?
Let b represent the number of either red or white balls. 11 ≤ b.
The probability of choosing 8 red balls and 11 white balls is the product of choosing 8 out of b red balls and 11 out of b white balls, divided by choosing 19 out of 2b total balls.
The value of b which results in the highest probability is the best guess, given no other information.
$$ = \dfrac{\dfrac{b!}{8!(b-8)!}\cdot\dfrac{b!}{11!(b-11)!}}{\dfrac{(2b)!}{19!(2b-19)!}}$$
Applying a little rearranging...
$$ = \dfrac{\dfrac{19!}{8!11!}\cdot\dfrac{(2b-19)!}{(b-11)!(b-8)!}}{\dfrac{(2b)!}{b!b!}}$$
$$= \dfrac{{19 \choose 8}\cdot{{2b-19} \choose {b-8}}}{{2b} \choose b}$$
This expression is the same as the beginning if b = 19. It also occured to me that the opposite, 11 red balls and 8 white balls remain in the urn.
Not convinced that this is the answer, I graphed the probabilities from 11 to 40.

38 balls seems to be the best guess.