Solution¶
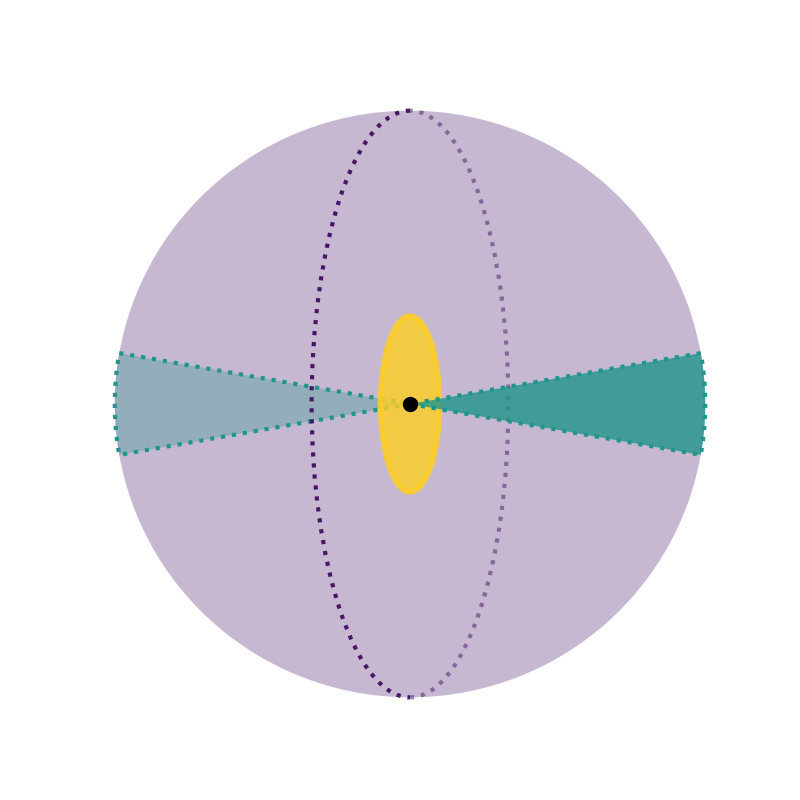
Consider the black hole, accretion disk, and two regions of being within 10° of perpendicular to the accretion disk.
Note that the two regions are identical spherical sectors, with sector angles of 20°.
Data from the Event Horizon Telescope was recently used to generate a never-before-seen image of the black hole — Sagittarius A* — at the center of our galaxy. One of the most striking things about the image is how clearly we can make out the black hole’s shadow (as shown below). That’s because the plane of its accretion disk is nearly perpendicular to the vector between us and the black hole.
We finally have the first look at our Milky Way black hole, Sagittarius A*. It’s the dawn of a new era of black hole physics. Credit: EHT Collaboration. #OurBlackHole #SgrABlackHole
— Event Horizon 'Scope (@ehtelescope) May 12, 2022
Link: https://t.co/Ax7ECRVg8A pic.twitter.com/LRWizSYOy9
Was this likely to occur, or was it just a cosmic coincidence? Let’s find out. Assuming the accretion disk was equally likely to be in any plane, what is the probability of it being within 10 degrees of perpendicular to us, thereby resulting in a spectacular image?
Consider the black hole, accretion disk, and two regions of being within 10° of perpendicular to the accretion disk.
Note that the two regions are identical spherical sectors, with sector angles of 20°.

Spherical sectors have $V = \dfrac{2\pi R^3(1-\cos \varphi)}{3}$, where $\varphi$ is half the sector angle.
Since there are two, and the volume of a sphere is $\dfrac{4\pi R^3}{3}$, the probability of the image is thus,
$$\dfrac{2\cdot\dfrac{2\pi R^3(1-\cos \varphi)}{3}}{\dfrac{4\pi R^3}{3}}$$
which simplifies quite nicely to
$$1-\cos \varphi$$
Since $\varphi = 10^{\circ}$, the probability $\approx 0.0152$.