I also ran the code for 1000 floors. I have plotted the first 100 below.
γ is the Euler-Mascheroni Constant.
From Starvind comes a matter of a frustrating (but not terrifying) tower:
You are on the 10th floor of a tower and want to exit on the first floor. You get into the elevator and hit 1. However, this elevator is malfunctioning in a specific way. When you hit 1, it correctly registers the request to descend, but it randomly selects some floor below your current floor (including the first floor). The car then stops at that floor. If it’s not the first floor, you again hit 1 and the process repeats.
Assuming you are the only passenger on the elevator, how many floors on average will it stop at (including your final stop, the first floor) until you exit?
Lets look at towers with fewer floors, where you start at the top and have to reach the 1st.
If there is only one floor, you would stop at 0 floors.
If there are only two floors, you would stop at exactly 1 floor.
If there are only three floors:
On average, you would be expected to stop at 1.5 floors.
There is a clear recursive definition:
On average, the expected number of stops can be expressed as:
$$EV(f) = \dfrac{1}{f-1} \cdot \sum\limits_{n=1}^{f-1} (1 + EV(n))$$
$$EV(f) = \dfrac{1}{f-1} \cdot \sum\limits_{n=1}^{f-2} (1 + EV(n)) + \dfrac{1 + EV(f-1)}{f-1}$$
$$EV(f) = \dfrac{f-2}{f-1} \cdot EV(f-1) + \dfrac{1 + EV(f-1)}{f-1}$$
$$EV(f) = \dfrac{(f-1)\cdot EV(f-1) +1}{f-1}$$
$$EV(f) - EV(f-1) = \dfrac{1}{f-1}$$
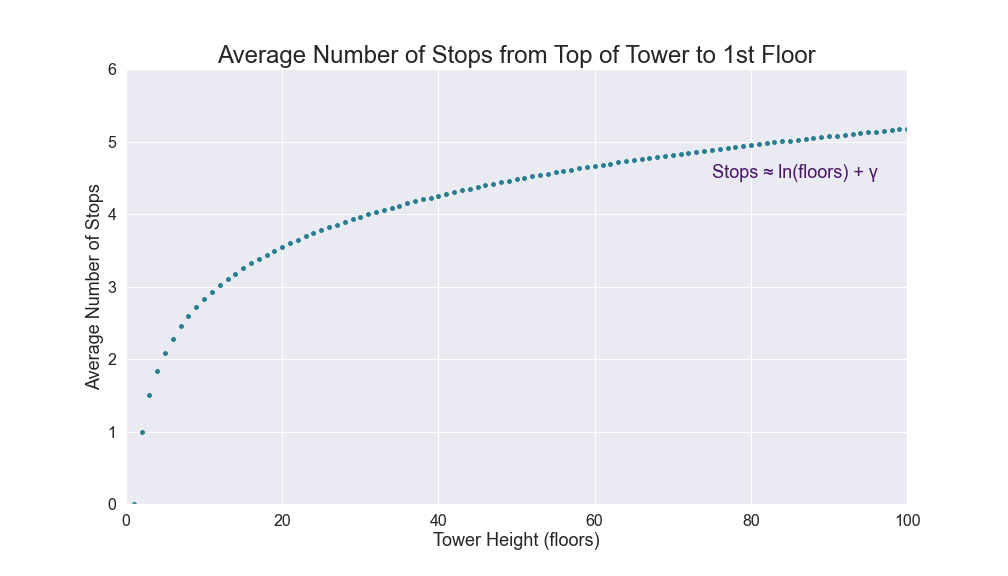
Since $\dfrac{\partial EV}{\partial f} \approx \dfrac{1}{f}$, the number of stops should be directly proportional to the natural log of floors.
For 10 floors, the exact expected average is $\dfrac{7129}{2520} \approx 2.829$ floors.
I also ran the code for 1000 floors. I have plotted the first 100 below.

γ is the Euler-Mascheroni Constant.