Solution¶
I ran some code:
- First I determined all the primes within a range.
- I then created a pxp array of the primes.
- If the row and column were the same, the cell was set to 1 (Getting from a prime to itself is a ladder of 1).
- If the row and column differ by one digit, the cell was set to 2.
- From there I ran a loop to combine ladders p1<->p2 and p2<->p3 to determine the value of ladder p1<->p3.
- This was continued until no cell had a missing value.
- The distribution of all optimal prime ladders was determined. Here is that of Two-Digit.
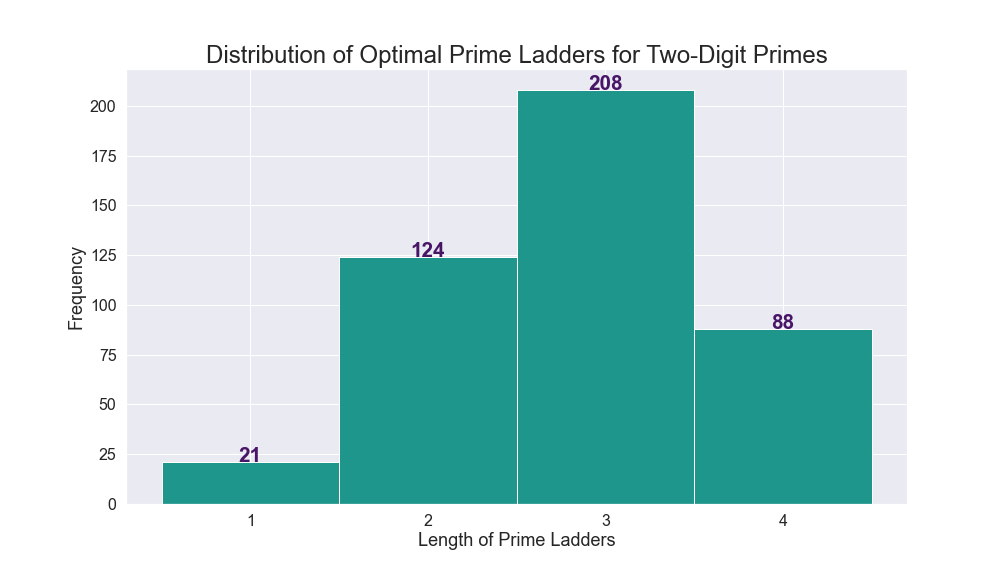
- I was able to determine the first and last primes in the longest optimal ladders.
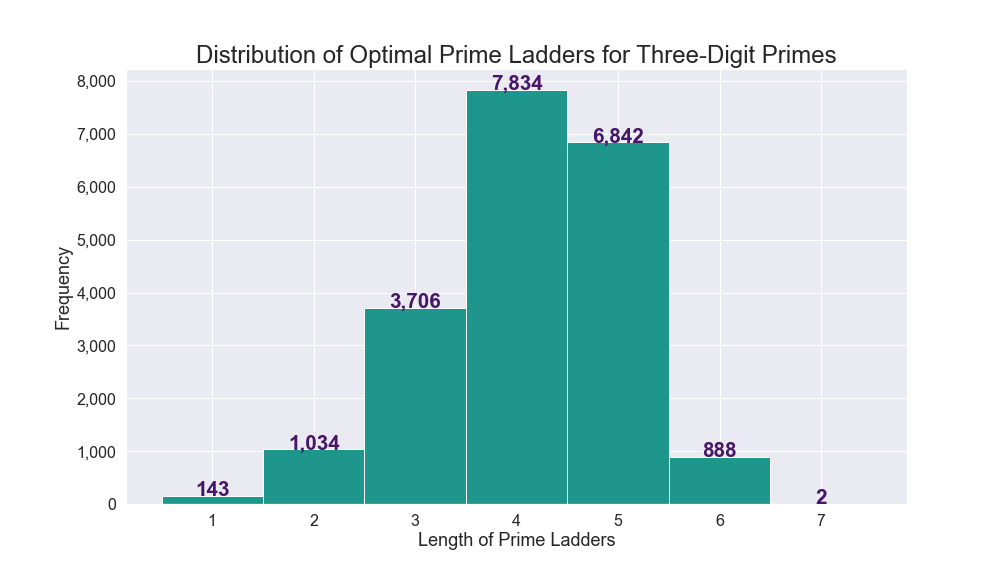 </li>
</li>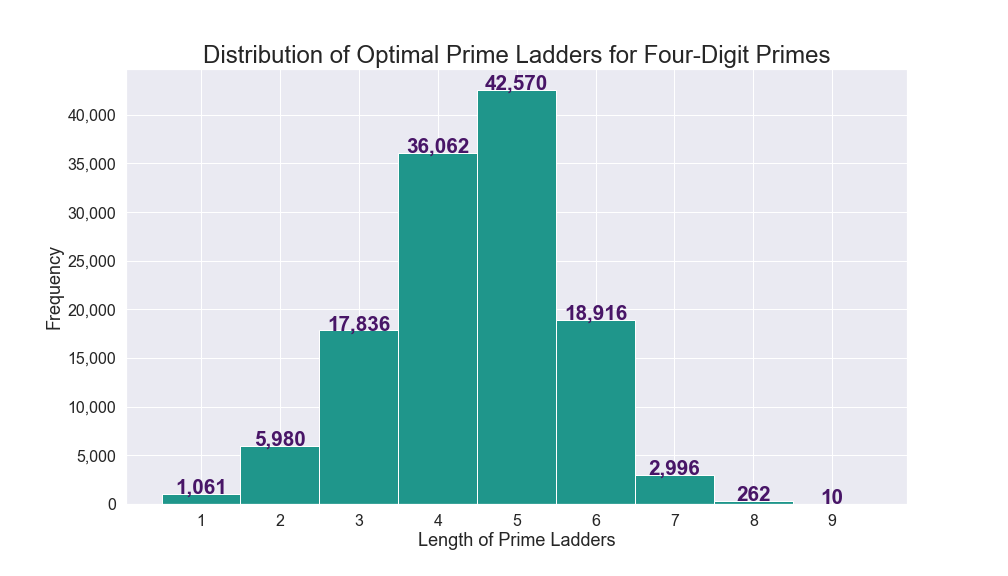 </li>
</li>