Can The Flash Beat The Bolt?

Riddler Express

The Flash challenges Usain Bolt to a 100-meter race. Bolt runs at an average speed of 10 meters per second. To make it interesting, the Flash decides he will pick a random speed between 5 meters per second and 16 meters per second, with each speed in between being equally likely. (Note that fractional and decimal speeds are included here, rather than just whole numbers.)

On average, how often would you expect the Flash to win? What would be his average margin of victory?

Solution

If The Flash chooses between 5 - 10 m/s, Bolt will win.

If The Flash chooses between 10 - 16 m/s, The Flash will win.

The Flash wins $\dfrac {6}{11}$ of the time.

Let $s_F$ represent The Flash's speed. The time The Flash takes to finish is thus $t_F = \dfrac{100}{s_F}$.

Since Bolt always requires 10 seconds, the difference can be represented as $10 - \dfrac{100}{s_F}$

The average margin of victory can be represented as,
$$\dfrac{1}{16-10} \cdot \int\limits_{s_F = 10}^{16} 10 - \dfrac{100}{s_F}$$
$$ = \dfrac{1}{6} \cdot \bigg[10s_F - 100\ln{s_F}\bigg]_{10}^{16} $$
$$ = \dfrac{1}{6} \cdot \bigg[\left(160 - 100\ln{16}\right) - \left(100 - 100\ln{10}\right) \bigg]$$
$$ = \dfrac{60 - 100\ln {\dfrac{8}{5}}}{6} \approx 2.17 \text{ seconds}$$

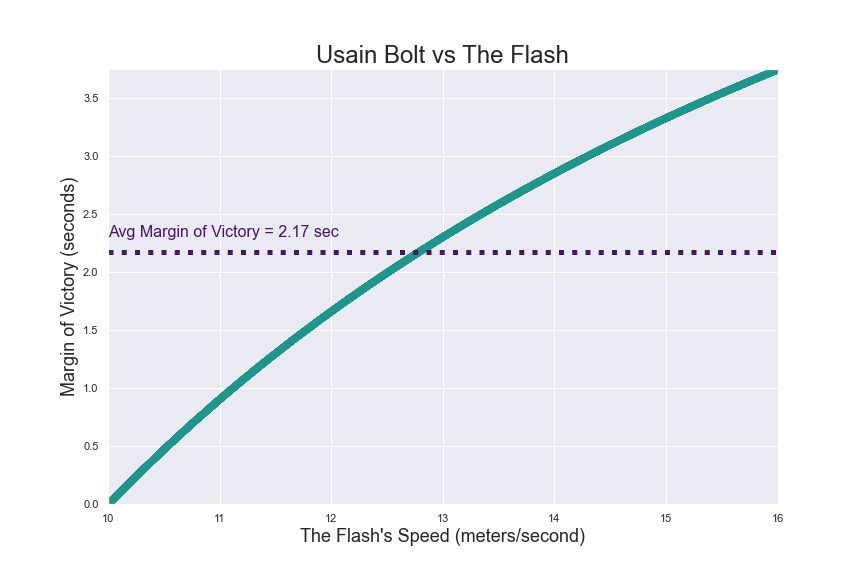
Since Bolt runs at 10 m/s, the average margin of victory can also be expressed as 21.7 meters.

Rohan Lewis

2022.04.24

Code can be found here.