I. Three cross sections are in the same hemisphere.¶

The astronomers of Planet Xiddler are back at it. They have developed a new technology for measuring the radius of a planet by analyzing its cross sections.
And so, they launch a satellite to study a newly discovered, spherical planet. The satellite sends back data about three parallel, equally spaced circular cross sections which have radii A, B and C megameters, with 0 < A < B < C. Based on these values, the scientists calculate the radius of the planet is R megameters. To their astonishment, they find that A, B, C and R are all whole numbers!
What is the smallest possible radius of the newly discovered planet?
There are 3 cases to look at.

Adding a few segments and labels yields:

Note that:
$$\sqrt{R^2 - B^2} - \sqrt{R^2 - C^2} = \sqrt{R^2 - A^2} - \sqrt{R^2 - B^2} = d$$I ran code to determine when this occurs, where $A < B < C < R$.
The smallest radius is $R = 14$ with $A = 7$, $B = 11$, $C = 13$, and $d = \sqrt{5}$

Adding a few segments and labels yields:

Note that:
$$\sqrt{R^2 - B^2} = \sqrt{R^2 - A^2} - \sqrt{R^2 - B^2} = d$$I ran code to determine when this occurs, where $A < B < C = R$.
The smallest radius is $R = 8$ with $A = 2$, $B = 7$, $C = 8$, and $d = \sqrt{15}$

Adding a few segments and labels yields:
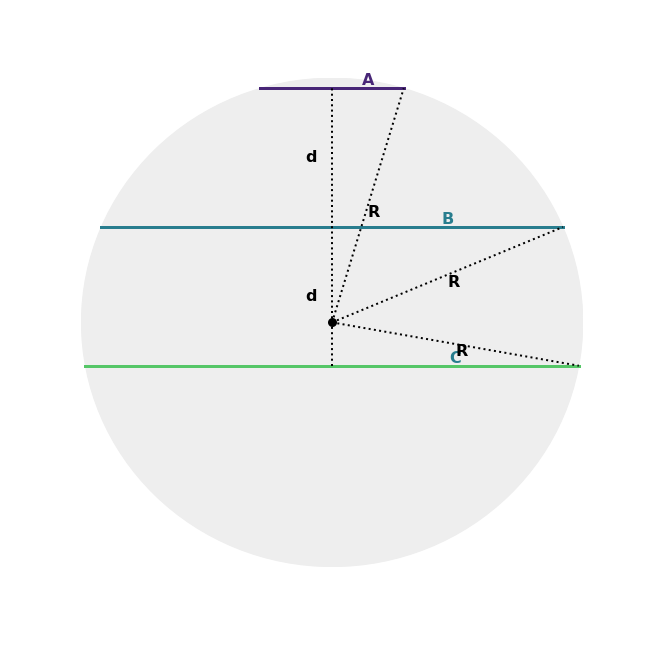
Note that:
$$\sqrt{R^2 - B^2} + \sqrt{R^2 - C^2} = \sqrt{R^2 - A^2} - \sqrt{R^2 - B^2} = d$$I ran code to determine when this occurs, where $A < B < C < R$.
The smallest radius is $R = 63$ with $A = 18$, $B = 58$, $C = 62$, and $d = 16\sqrt{5}$
The smallest radius is 8.