Solution¶
There are $6^4 = 1296$ possibilities outcomes of 4 dice rolls.
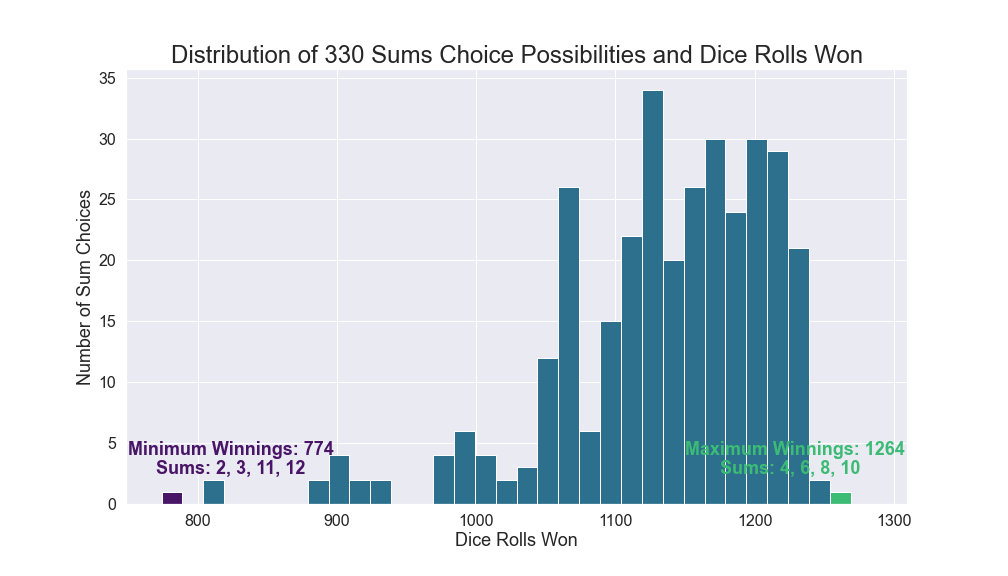
There are $ {11 \choose 4} = 330$ ways of chosing 4 sums.
There will be a subset of outcomes remaining which is dependent on the sum chosen and highly variable.
I wrote some code. For each of the sum possibilities, it looked at all 1296 outcomes and successively eliminated outcomes won for the unique combination of 4 numbers.