Answer¶
$y = \dfrac{y_2(x-x_1)^2 - y_1(x-x_2)^2}{(x_1^2 - x_2^2)- 2x(x_1 - x_2)}$
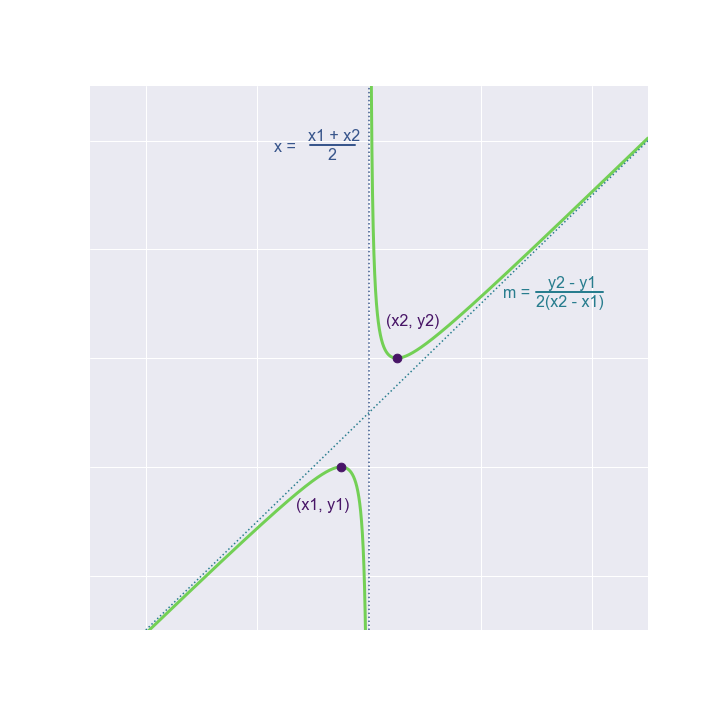This equation has some interesting characteristics.
From Sean Sweeney, Chris Nho and Eli Luberoff comes a Classic that is for anyone who ever thought even more deeply about functions in high school algebra.
Suppose you have two distinct points on the x-axis of the coordinate plane. If I tell you a parabola passes through those two points, where on the plane could that parabola’s vertex be? Spoiler alert: The vertex can be anywhere on the perpendicular bisector of those two points. (Neat!)
Now, suppose the two distinct points are anywhere on the coordinate plane. If I tell you that a parabola with a vertical line of symmetry passes through those two points, where on the plane could that parabola’s vertex be?
Consider a parabola and two points it contains, $(x_1, y_1)$ and $(x_2, y_2)$.
We have the following three equations.
$$y = ax^2 + bx + c$$$$y_1 = ax_1^2 + bx_1 + c$$$$y_2 = ax_2^2 + bx_2 + c$$Subtracting either of the second or third from the first yields the following two equations.
$$y - y_1 = a(x^2 - x_1^2) + b(x - x_1)$$$$y - y_2 = a(x^2 - x_2^2) + b(x - x_2)$$Multiplying the first by $(x-x_2)$ and second by $(x-x_1)$ to eliminate b,
$$(y - y_1)(x - x_2) = a(x^2 - x_1^2)(x - x_2) + b(x - x_1)(x - x_2)$$$$(y - y_2)(x - x_1) = a(x^2 - x_2^2)(x - x_1) + b(x - x_2)(x - x_1)$$$$(y - y_1)(x - x_2) - (y - y_2)(x - x_1) = a(x^2 - x_1^2)(x - x_2) - a(x^2 - x_2^2)(x - x_1)$$$$y(x_1 - x_2) - x(y_1 - y_2) - (x_1y_2 - x_2y_1) = a(x - x_1)(x - x_2)(x_1-x_2)$$$\dfrac{y(x_1 - x_2) - x(y_1 - y_2) - (x_1y_2 - x_2y_1)}{(x - x_1)(x - x_2)(x_1 - x_2)} = a$
Multiplying the first by $(x^2 - x_2^2)$ and second by $(x^2 - x_1^2)$ to eliminate a,
$$(y - y_1)(x^2 - x_2^2) = a(x^2 - x_1^2)(x^2 - x_2^2) + b(x - x_1)(x^2 - x_2^2)$$$$(y - y_2)(x^2 - x_1^2) = a(x^2 - x_2^2)(x^2 - x_1^2) + b(x - x_2)(x^2 - x_1^2)$$$$(y - y_1)(x^2 - x_2^2) - (y - y_2)(x^2 - x_1^2) = b(x - x_1)(x^2 - x_2^2) - b(x - x_2)(x^2 - x_1^2)$$$$y(x_1^2 - x_1^2) - x^2(y_1 - y_2) - (x_1^2y_2 - x_2^2y_1) = -b(x - x_1)(x - x_2)(x_1 - x_2)$$$-\dfrac{y(x_1^2 - x_2^2) - x^2(y_1 - y_2) - (x_1^2y_2 - x_2^2y_1)}{(x - x_1)(x - x_2)(x_1-x_2)} = b$
Substituting into the vertex equation $\dfrac{-b}{2a} = x$,
$$ \dfrac{\dfrac{y(x_1^2 - x_2^2) - x^2(y_1 - y_2) - (x_1^2y_2 - x_2^2y_1)}{(x - x_1)(x - x_2)(x_1-x_2)}}{2 \cdot \dfrac{y(x_1 - x_2) - x(y_1 - y_2) - (x_1y_2 - x_2y_1)}{(x - x_1)(x - x_2)(x_1 - x_2)}} = x$$Eliminating the common denominators,
$$y(x_1^2 - x_2^2) - x^2(y_1 - y_2) - (x_1^2y_2 - x_2^2y_1) = 2xy(x_1 - x_2) - 2x^2(y_1 - y_2) - 2x(x_1y_2 - x_2y_1)$$$$y(x_1^2 - x_2^2) - 2xy(x_1 - x_2) = - x^2(y_1 - y_2) - 2x(x_1y_2 - x_2y_1) + (x_1^2y_2 - x_2^2y_1)$$$$y\big((x_1^2 - x_2^2) - 2x(x_1 - x_2) \big) = y_2(x^2 - 2xx_1 + x_1^2) - y_1(x^2 - 2xx_2 + x_2^2)$$$y = \dfrac{y_2(x-x_1)^2 - y_1(x-x_2)^2}{(x_1^2 - x_2^2)- 2x(x_1 - x_2)}$
This equation has some interesting characteristics.
Substitute $x = x_1$,
$$y = \dfrac{y_2(x_1-x_1)^2 - y_1(x_1-x_2)^2}{(x_1^2 - x_2^2) - 2x_1(x_1 - x_2)}$$$$y = \dfrac{0 - y_1(x_1-x_2)^2}{(-x_1^2 + 2x_1x_2 - x_2^2)}$$$$y = \dfrac{-y_1(x_1-x_2)^2}{-(x_1-x_2)^2} = y_1$$Similarly, substitute $x = x_2$,
$$y = \dfrac{y_2(x_2-x_1)^2 - y_1(x_2-x_2)^2}{(x_1^2 - x_2^2) - 2x_2(x_1 - x_2)}$$$$y = \dfrac{y_2(x_2-x_1)^2}{(x_1^2 - 2x_1x_2 + x_2^2)}$$$$y = \dfrac{y_2(x_2-x_1)^2}{(x_1-x_2)^2} = y_2$$Setting the denominator $ = 0$,
$$(x_1^2 - x_2^2)- 2x(x_1 - x_2) = 0$$$$x = \dfrac{-(x_1^2 - x_2^2)}{-2(x_1 - x_2)}$$$$x = \dfrac{x_1 + x_2}{2}$$Note this is half the slope of the two initial points.
The equation of this line is $y - \dfrac{y_2 + y_1}{2} = \dfrac{y_2 - y_1}{2(x_2 - x_1)} \cdot \left(x - \dfrac{x_2 + x_1}{2} \right)$