c coins¶
Here is a recursive general form for $c$ coins.
- 0 heads - $\dfrac{1}{2^c}\cdot\left(1 + \left(\dfrac{1}{2^c}\right)^1 + \left(\dfrac{1}{2^c}\right)^2 + ...\right) = \dfrac{1}{2^c-1}$
- 1 heads - $\dfrac{c}{8}\cdot\left(1 + \left(\dfrac{1}{2^c}\right)^1 + \left(\dfrac{1}{2^c}\right)^2 + ...\right) = \dfrac{c}{2^c-1}$
- 2 heads - $\dfrac{c(c-1)}{2^c}\cdot\left(1 + \left(\dfrac{1}{2^c}\right)^1 + \left(\dfrac{1}{2^c}\right)^2 + ...\right) = \dfrac{c^2-c}{2^c-1}$
- $ ... $
- $h$ heads - $\dfrac{\dfrac{c!}{(c-h)!h!}}{2^c}\cdot\left(1 + \left(\dfrac{1}{2^c}\right)^1 + \left(\dfrac{1}{2^c}\right)^2 + ...\right) = \dfrac{c!}{(c-h)!h!(2^c-1)}$
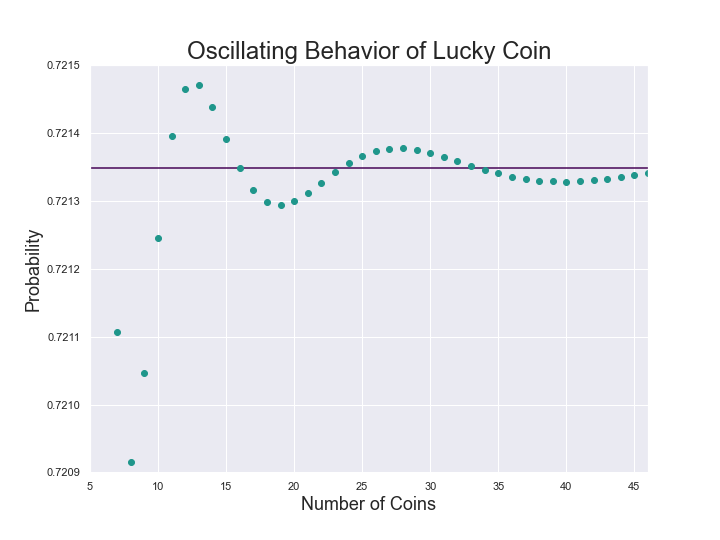
Using the number of coins and the probability of getting a single lucky coin yields the following expected value for $c$ coins
$$L(c) = \sum_{h=0}^{c-1} \dfrac{c!}{(c-h)!h!(2^c-1)} \cdot L(h)$$The following begins to show the asymptotic behavior of $L(c)$:
| $c$ | $L(c)$ | Decimal Approx. |
|---|---|---|
| $0$ | $0$ | $0$ |
| $1$ | $1$ | $1$ |
| $2$ | $\dfrac{2}{3}$ | $\approx 0.6666667$ |
| $3$ | $\dfrac{5}{7}$ | $\approx 0.7142857$ |
| $4$ | $\dfrac{76}{105}$ | $\approx 0.7238095$ |
| $5$ | $\dfrac{471}{651}$ | $\approx 0.7238095$ |
| $6$ | $\dfrac{470}{651}$ | $\approx 0.7219662$ |
| $7$ | $\dfrac{2839}{3937}$ | $\approx 0.7211074$ |