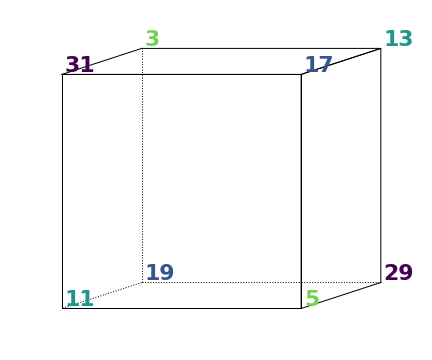
Using four pairs of some of the first few twin primes placed at opposite vertices, I achieved the following cube with face sum $=64$
From Dean Ballard comes a cubical conundrum:
Consider a cube, which has eight vertices, or corners. Suppose I assign a prime number to each vertex. A “face sum” is the value I get when I add up all four prime numbers on one of the six faces.
Can you find eight distinct primes and arrange them on a cube so that the six face sums are all equal?
Extra credit: Can you find another set of eight distinct primes that can similarly be arranged on the vertices of a cube? How many more can you find?
Using four pairs of some of the first few twin primes placed at opposite vertices, I achieved the following cube with face sum $=64$

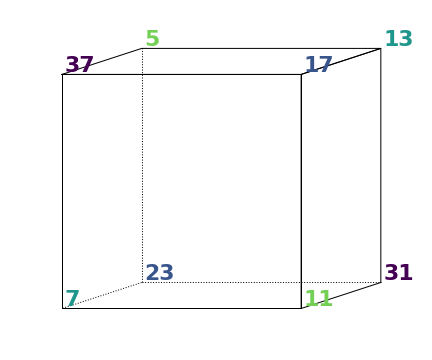
Using four pairs of some of the first few sexy primes placed at opposite vertices, I achieved the following cube with face sum $=72$
Based on the twin prime conjecture and nature of prime gaps, I believe there are an infinite number of such cubes.
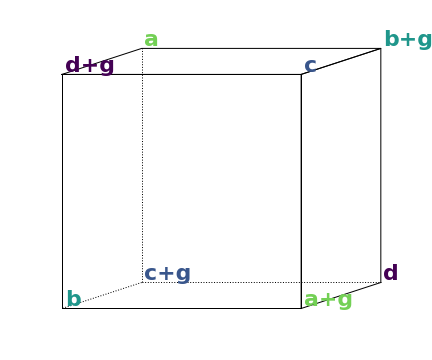
Using four pairs of primes with the same pairwise difference placed at opposite vertices, I achieved the following general form cube with face sum $=a+b+c+d+2g$