Can You Design The Perfect Wedding?

Riddler Classic

Rumor has it that readers of The Riddler Ellora Sarkar and Daniel Gomez are getting married this weekend. Congratulations to you both! In keeping with the hexagonal design of your wedding backdrop, I thought you might enjoy the following puzzle. (Riddler Nation, this one’s for you, too!)

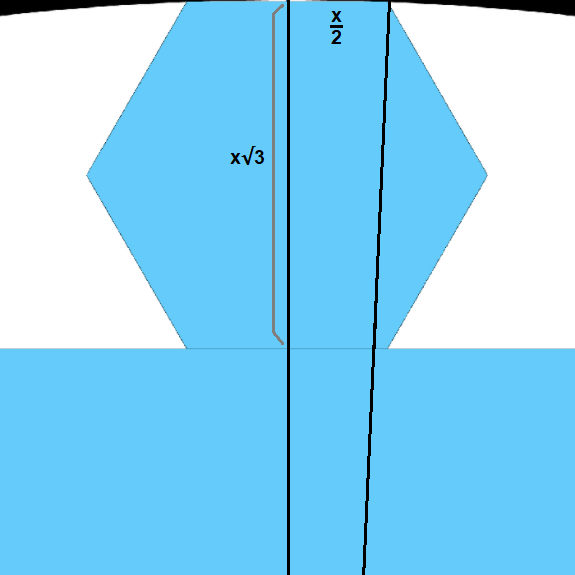
The larger regular hexagon in the diagram below has a side length of 1.

What is the side length of the smaller regular hexagon?

Extra credit: If you look very closely, there are two more, even smaller hexagons on top. Can you see them? No? Maybe this animation will help:

What are the side lengths of these two even smaller hexagons?

Solution

A hexagon inscribed a circle has a side length same as the radius of the aforementioned circle.

Therefore, Any vertex on any hexagon that lies on the circle is 1 from the center.

For any subsequent hexagon, a right triangle can be used to determine the side length.
$$\left(\dfrac{x}{2}\right)^2 + \left(x\sqrt3 + H \right)^2 = 1$$
where $H$ is the length of the apothem(s) of the previous hexagon(s) until the center of the circle is reached.

For the second Hexagon, $H = \dfrac{\sqrt{3}}{2}$
$$\left(\dfrac{x}{2}\right)^2 + \left(x\sqrt3 + \dfrac{\sqrt{3}}{2} \right)^2 = 1$$
$$(x)^2 + 3(2x + 1)^2 = 4$$
$$x^2 + 12x^2 + 12x + 3 = 4$$
$$13x^2 + 12x - 1 = 0$$
$$(13x - 1)(x + 1) = 0$$
$$x = \dfrac{1}{13}$$

For the third Hexagon, $H = \dfrac{\sqrt{3}}{2} + \dfrac{\sqrt{3}}{13} = \dfrac{15 \sqrt{3}}{26}$
$$\left(\dfrac{x}{2}\right)^2 + \left(x\sqrt3 + \dfrac{15 \sqrt{3}}{26}\right)^2 = 1$$
$$(13x)^2 + 3(26x + 15)^2 = 26^2$$
$$169x^2 + 2028x^2 + 2340x + 675 = 676$$
$$2197x^2 + 2340x - 1 = 0$$
$$x = \dfrac{\sqrt{8113}-90}{169}$$

Answer:

Continuing yields a decimal approximation for the 4th Hexagon side length.

Hexagon	Side Length
1	$1$
2	$\dfrac{1}{13} \approx 7.692 \cdot 10^{-2}$
3	$\dfrac{\sqrt{8113}-90}{169} \approx 4.271 \cdot 10^{-4}$
4	$\approx 1.317 \cdot 10^{-8}$

Rohan Lewis

2022.01.24

Code can be found here.