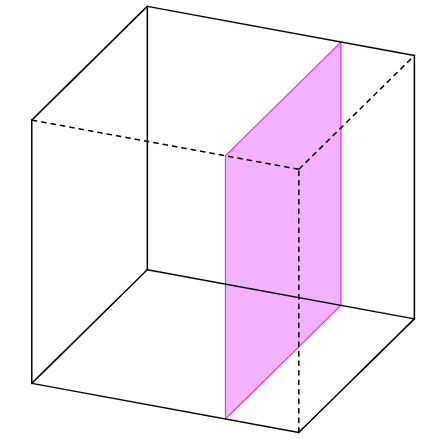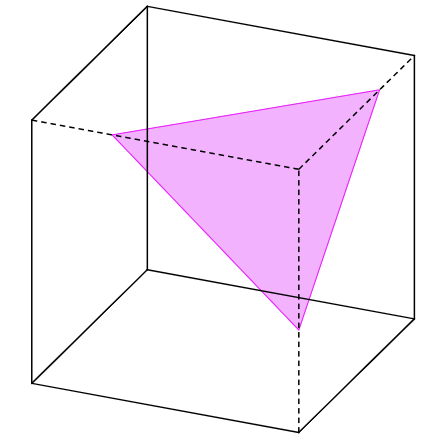
Surface Area¶
Three isosceles right triangles, each of area $\dfrac{x^2}{2}$ are missing from the cube. A new equilateral triangle of area $\dfrac{x^2\sqrt{3}}{4}$ is added.
$$SA = 6 - \dfrac{3x^2}{2} + \dfrac{x^2\sqrt{3}}{4}$$
$$SA = \dfrac{24 + \left(\sqrt{3} - 6\right)x^2}{4}$$
Volume¶
The volume of the missing triangular pyramid is $\dfrac{x^3}{6}$.
$$V = 1 - \dfrac{x^3}{6}$$
$$= \dfrac{6-x^3}{6}$$
Ratio¶
$$\dfrac{SA}{V} = \dfrac{\dfrac{24 + \left(\sqrt{3} - 6\right)x^2}{4}}{\dfrac{6-x^3}{6}}$$
$$= \dfrac{72 + \left(3\sqrt{3} - 18\right)x^2}{12-2x^3}$$
Taking the derivative,
$$0 = \dfrac{\left(12-2x^3\right)\left(6\sqrt{3}x-36x\right) - \left(72 + \left(3\sqrt{3} - 18\right)x^2\right)\left(-6x^2\right)}{\left(12-2x^3\right)^2}$$
Using WolframAlpha yields $x \approx 0.73485$, resulting in a minimum ratio of $5.8079$.