Can You Survive Squid Game Riddler?

Riddler Classic

From Arnaud Quentin comes a question that recent took Netflix subscribers by squid — I mean storm:

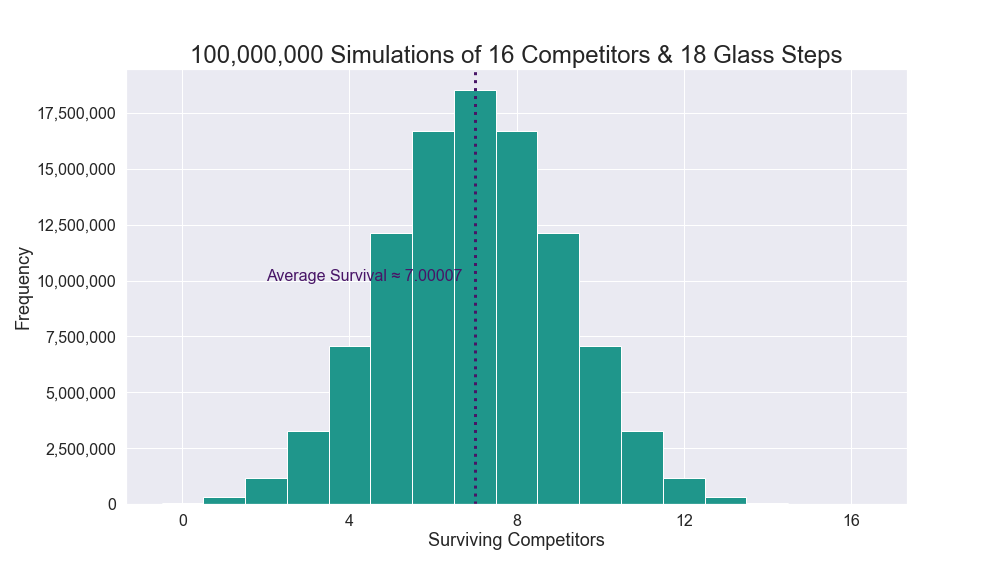
Congratulations, you’ve made it to the fifth round of The Squiddler — a competition that takes place on a remote island. In this round, you are one of the 16 remaining competitors who must cross a bridge made up of 18 pairs of separated glass squares. Here is what the bridge looks like from above:

To cross the bridge, you must jump from one pair of squares to the next. However, you must choose one of the two squares in a pair to land on. Within each pair, one square is made of tempered glass, while the other is made of normal glass. If you jump onto tempered glass, all is well, and you can continue on to the next pair of squares. But if you jump onto normal glass, it will break, and you will be eliminated from the competition.

You and your competitors have no knowledge of which square within each pair is made of tempered glass. The only way to figure it out is to take a leap of faith and jump onto a square. Once a pair is revealed — either when someone lands on a tempered square or a normal square — all remaining competitors take notice and will choose the tempered glass when they arrive at that pair.

On average, how many of the 16 competitors will survive and make it to the next round of the competition?

Solution

Let $EV(c, g)$ represent the average number of $c$ competitors that survive $g$ glass squares on a bridge.

I came up with an explicit definition and a recursive definition.

Explicit

The number of deaths can be anywhere from 0 to the number of competitors.

• There can be any possibility of deaths among the steps.
• The probability of each step breaking or holding is $\dfrac{1}{2}$.
• The number of survivors is competitors minus deaths.

This can be represented as:
$$EV(c, g) = \sum_{d=0}^c {g \choose d} \left(\frac{1}{2}\right)^g \left(c - d\right)$$

Note

If there are more competitors than steps, then any competitor whose place is greater than the number of steps will always have enough information to cross.

This can be represented as:
$$EV(c, g) = c-g + EV(g,g)$$
Since $d$ deaths and $g-d$ survivors have the same probability as $g-d$ deaths and $d$ survivors, it follows that $EV(g,g) = \dfrac{g}{2}$.

Thus for $c \ge g$:
$$EV(c, g) = c - \dfrac{g}{2}$$

Recursive

No one is left.

Everyone has died, or $EV(0, g) = 0$

No steps are left.

Everyone remaining lives, or $EV(c, 0) = c$

All other scenarios.

Half the time the current competitor will die on the current step, leaving $c-1$ competitors and $g-1$ steps.

Half the time the current competitor will live on the current step, leaving $c$ competitors and $g-1$ steps.

This can be represented as:
$$EV(c, g) = \frac{1}{2}EV(c-1, g-1) + \frac{1}{2}EV(c, g-1)$$

Table

Both the explicit and recursive yielded the same results.

		g
		1	2	3	4	5	6
c	1	$$\dfrac{1}{2}$$	$$\dfrac{1}{4}$$	$$\dfrac{1}{8}$$	$$\dfrac{1}{16}$$	$$\dfrac{1}{32}$$	$$\dfrac{1}{64}$$
	2	$$\dfrac{3}{2}$$	$$1$$	$$\dfrac{5}{8}$$	$$\dfrac{3}{8}$$	$$\dfrac{7}{32}$$	$$\dfrac{1}{8}$$
	3	$$\dfrac{5}{2}$$	$$2$$	$$\dfrac{3}{2}$$	$$\dfrac{17}{16}$$	$$\dfrac{23}{32}$$	$$\dfrac{15}{32}$$
	4	$$\dfrac{7}{2}$$	$$3$$	$$\dfrac{5}{2}$$	$$2$$	$$\dfrac{49}{32}$$	$$\dfrac{9}{8}$$
	5	$$\dfrac{9}{2}$$	$$4$$	$$\dfrac{7}{2}$$	$$3$$	$$\dfrac{5}{2}$$	$$\dfrac{129}{64}$$
	6	$$\dfrac{11}{2}$$	$$5$$	$$\dfrac{9}{2}$$	$$4$$	$$\dfrac{7}{2}$$	$$3$$

Answer

$$EV(16, 18) = \dfrac{1835028}{262144} \approx 7.0000763 \text{ competitors}$$

I also ran a simulation of 100,000,000 trials and achieved a similar result.

Rohan Lewis

2021.10.31

Code can be found here.