From Allen Gu comes a geometric puzzle that he recalls from a university challenge:
Suppose you have an equilateral triangle. You pick three random points, one along each of its three edges, uniformly along the length of each edge — that is, each point along each edge has the same probability of being selected.
With those three randomly selected points, you can form a new triangle inside the original one. What is the probability that the center of the larger triangle also lies inside the smaller one?
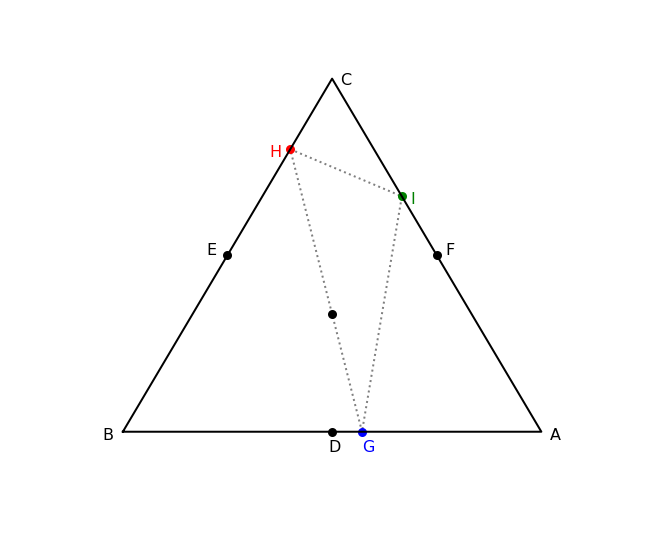
Equilateral $\triangle ABC$ with midpoints $D, E, F$.
Let:
Setting the triangle with unit lengths, the following coordinates can be used.
| Point | Coordinate |
|---|---|
| A | $\left(1, 0 \right)$ |
| B | $\left(0, 0 \right)$ |
| C | $\left(\dfrac {1}{2}, \dfrac{\sqrt {3}}{2} \right)$ |
| Center | $\left(\dfrac {1}{2}, \dfrac {\sqrt {3}}{6} \right)$ |
| D | $\left(\dfrac {1}{2}, 0 \right)$ |
| E | $\left(\dfrac {1}{4}, \dfrac{\sqrt {3}}{4} \right)$ |
| F | $\left(\dfrac {3}{4}, \dfrac{\sqrt {3}}{4} \right)$ |
| $G$ | $\left(x_G, y_G \right)$ |
| $H$ | $\left(x_H, y_H \right)$ |
$\triangle GHI$ will always contain the center. This case can happen in 3 mutally exclusive ways:
The calculated probability will be multiplied by $3$ to include all subcases.
Using $B$ and $C$,
$$y = x\sqrt{3}$$Combining the two above,
$$x_H\sqrt{3}= y_H = \frac{\sqrt{3}}{3-6x_G}x_H - \frac{x_G\sqrt{3}}{3-6x_G}$$
$$x_H = \frac{x_H}{3-6x_G} - \frac{x_G}{3-6x_G}$$
$$3x_H - 6x_Gx_H = x_H - x_G$$
$$x_H(3 - 6x_Gx - 1) = - x_G$$
$$x_H = \frac{x_G}{-2+6x_G}$$
$G$ can be any point on $AD$, $H$ can be any point between $\dfrac{1}{4}$ from $E$ and the value of $x_H$ defined by $x_G$ from above, and $I$ can be any point on $CA$. Multiplying the probabilities of $H$ and $I$ for each $G$,
$$y = 3\int_{x_G = \frac{1}{2}}^{1} \left(x_H - \frac{1}{4} \right) \cdot 1 \cdot dx_G$$
$$= 3\int_{x_G = \frac{1}{2}}^{1} \left(\frac{x_G}{-2+6x_G} - \frac{1}{4} \right)dx_G$$
$$= 3\int_{x_G = \frac{1}{2}}^{1} \frac{2x_G - 1(-1+3x_G)}{-4+12x_G}dx_G$$
$$= \frac{1}{4}\int_{x_G = \frac{1}{2}}^{1} \frac{-3x_G + 3}{3x_G - 1}dx_G$$
$$= \frac{1}{4}\int_{x_G = \frac{1}{2}}^{1} -1 + \frac{2}{3x_G - 1} dx_G$$
$$=\frac{1}{4}\left(\left.-x_G +\frac{2}{3}\ln{(3x_G-1)}\right|_\frac{1}{2}^1\right)$$
$$=\frac{1}{4}\left(\left(-1 + \frac{2}{3}\ln{2} \right) - \left(-\frac{1}{2} + \frac{2}{3}\ln{\frac{1}{2}} \right)\right)$$
$$=\frac{1}{4}\left(\frac{4}{3}\ln{2} - \frac{1}{2}\right)$$
$$=\frac{1}{3}\ln{2} - \frac{1}{8}$$
Adding the probabilities from Case I,
$$=\frac{1}{3}\ln{2} + \frac{1}{8} \approx 0.356$$