Answer¶
The expected value for four dice is:
$$\approx 18.8436$$
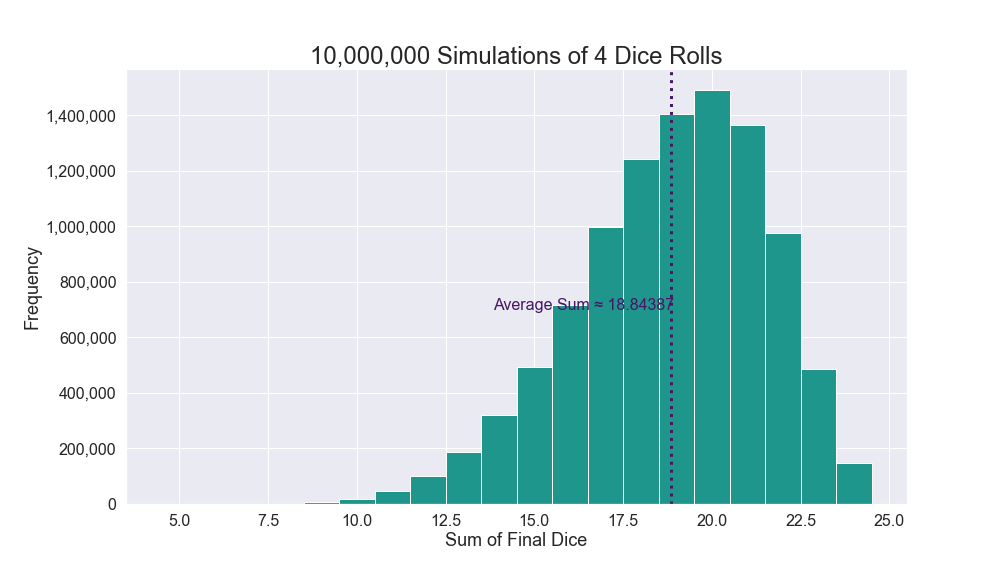
I also ran a simulation of 10,000,000 trials and achieved a similar result.
From Oliver Ruebenacker comes a “classic” indeed:
You have four standard dice, and your goal is simple: Maximize the sum of your rolls. So you roll all four dice at once, hoping to achieve a high score.
But wait, there’s more! If you’re not happy with your roll, you can choose to reroll zero, one, two or three of the dice. In other words, you must “freeze” one or more dice and set them aside, never to be rerolled.
You repeat this process with the remaining dice — you roll them all and then freeze at least one. You repeat this process until all the dice are frozen.
If you play strategically, what score can you expect to achieve on average?
Extra credit: Instead of four dice, what if you start with five dice? What if you start with six dice? What if you start with N dice?
A die should be kept if its face value is greater than the expected value of rolling one die.
Hence, always freeze all dice $>3$.
| Case Description | Probability | Average Sum |
|---|---|---|
| Both dice are $>3$ | $\dfrac{9}{36}$ | $2 \cdot \dfrac{4+5+6}{3} = 10$ |
| One die $>3$, one die $\le 3$ | $\dfrac{18}{36}$ | $\dfrac{4+5+6}{3} + EV(1) = 8.5$ |
| Both dice are $\le 3$, 3 is the maximum | $\dfrac{5}{36}$ | $3 + EV(1) = 6.5$ |
| Both dice are $\le 3$, 2 is the maximum | $\dfrac{3}{36}$ | $2 + EV(1) = 5.5$ |
| Both dice are $\le 3$, 1 is the maximum | $\dfrac{1}{36}$ | $1 + EV(1) = 4.5$ |
The expected value of two dice is:
Note that freezing a single 4 is advantageous, as $4 > EV(1)$.
Note that rerolling two 4s is advantageous, as $2 \cdot 4 < EV(2)$.
| Case Description | Probability | Average Sum |
|---|---|---|
| All dice $>4$ | $\dfrac{8}{216}$ | $3 \cdot \dfrac{5+6}{2} = 16.5$ |
| Two dice $>4$, one die $=4$ | $\dfrac{12}{216}$ | $2 \cdot \dfrac{5+6}{2} + 4 = 15$ |
| Two dice $>4$, one die $<4$ | $\dfrac{36}{216}$ | $2 \cdot\dfrac{5+6}{2} + EV(1) \approx 14.5$ |
| One die $>4$, two dice $\le 4$ | $\dfrac{96}{216}$ | $\dfrac{5+6}{2} + EV(2) \approx 13.7$ |
| Three dice are $\le 4$, 4 is the maximum | $\dfrac{37}{216}$ | $4 + EV(2) \approx 12.2$ |
| Three dice are $\le 4$, 3 is the maximum | $\dfrac{19}{216}$ | $3 + EV(2) \approx 11.2$ |
| Three dice are $\le 4$, 2 is the maximum | $\dfrac{7}{216}$ | $2 + EV(2) \approx 10.2$ |
| Three dice are $\le 4$, 1 is the maximum | $\dfrac{1}{216}$ | $1 + EV(2) \approx 9.2$ |
The expected value for three dice is:
Note that freezing a 5 is advantageous if rerolling one other die, as $5 + EV(1) > EV(2)$
Note that rerolling a 5 is advantageous if rerolling two other dice, as $5 + EV(2) < EV(3)$
| Case Description | Probability | Average Sum |
|---|---|---|
| All dice $>4$ | $\dfrac{16}{1296}$ | $4 \cdot \dfrac{5+6}{2} = 22$ |
| Three dice $>4$, one die $=4$ | $\dfrac{32}{1296}$ | $3 \cdot \dfrac{5+6}{2} + 4 = 20.5$ |
| Three dice $>4$, one die $<4$ | $\dfrac{96}{1296}$ | $3 \cdot\dfrac{5+6}{2} + EV(1) = 20$ |
| Two dice $=6$, two dice $\le4$ | $\dfrac{96}{1296}$ | $2 \cdot 6 + EV(2) \approx 20.2$ |
| One die $=6$, one die $=5$, two dice $\le4$ | $\dfrac{192}{1296}$ | $6 + EV(3) \approx 19.4$ |
| Two dice $=5$, two dice $\le4$ | $\dfrac{96}{1296}$ | $5 + EV(3) \approx 18.4$ |
| One die $=6$, three dice $\le4$ | $\dfrac{256}{1296}$ | $6 + EV(3) \approx 19.4$ |
| One die $=5$, three dice $\le4$ | $\dfrac{256}{1296}$ | $5 + EV(3) \approx 19.4$ |
| Four dice are $\le 4$, 4 is the maximum | $\dfrac{175}{1296}$ | $4 + EV(3) \approx 17.4$ |
| Four dice are $\le 4$, 3 is the maximum | $\dfrac{65}{1296}$ | $3 + EV(3) \approx 16.4$ |
| Four dice are $\le 4$, 2 is the maximum | $\dfrac{15}{1296}$ | $2 + EV(3) \approx 15.4$ |
| Four dice are $\le 4$, 1 is the maximum | $\dfrac{1}{1296}$ | $1 + EV(3) \approx 14.4$ |
The expected value for four dice is:
$$\approx 18.8436$$
I also ran a simulation of 10,000,000 trials and achieved a similar result.

I used a recursive algorithm to determine some more values.
The algorithm sorts the dice from largest to smallest. It freezes a single largest die.
It compares the sum of the remaining $n-1$ unfrozen dice with rerolling all of them.
It compares the sum of the largest remaining $n-2$ unfrozen dice and rerolling the smallest die with rerolling all of them.
It compares the sum of the largest remaining $n-3$ unfrozen dice and rerolling the smallest two dice with rerolling all of them.
...
The last comparison is the sum of the largest remaining die and rerolling the smallest $n-2$ dice with rerolling all of them.
If any of these $n-1$ comparisons are true, there is a reason to keep the largest die.
For $6,5,5,5,4$, the 6 is frozen.
$5+5+5+4 = 19 > EV(4)$, so a 5 is kept.
$5+5+4 = 14 > EV(3)$, so a 5 is kept.
$5+4 = 9 > EV(2)$, so the 5 is kept.
$4 > EV(1)$, so the 4 is kept.
However, notice that for $6,5,5,5,3$, it begins the same, freezing the 6.
$5+5+5+3 < EV(4)$.
$5+5+5+ EV(1) < EV(4)$.
$5+5+EV(2) < EV(4)$.
$5+EV(3) < EV(4)$.
Since rerolling all 4 unfrozen is advantageous in every comparison, the four remaining dice are rerolled.
For 5 dice, the maximum sum $\approx 24.436$
For 6 dice, the maximum sum $\approx 30.153$
It seems for large $N$, it is advantageous to only freeze 6s until only a few dice remain. I do not know the cutoff.
For large $N$, the answer seems to be $\approx 6N - 6$.