Can You Zoom Around The Race Track?

Riddler Classic

The game of RaceTrack was published by recreational mathematician Martin Gardner in 1973. There have been a few modifications and even some neat digital versions since then, and it’s high time we had a race here on The Riddler.

So without further ado, welcome to the Riddler-opolis 500!

You begin at the midpoint of the starting line at the bottom (the thicker border), and your goal is to circumnavigate the race track shown below in a single counterclockwise loop. You’ll be moving from point to point on the grid, without ever venturing into the gray surrounding square or the central circle.

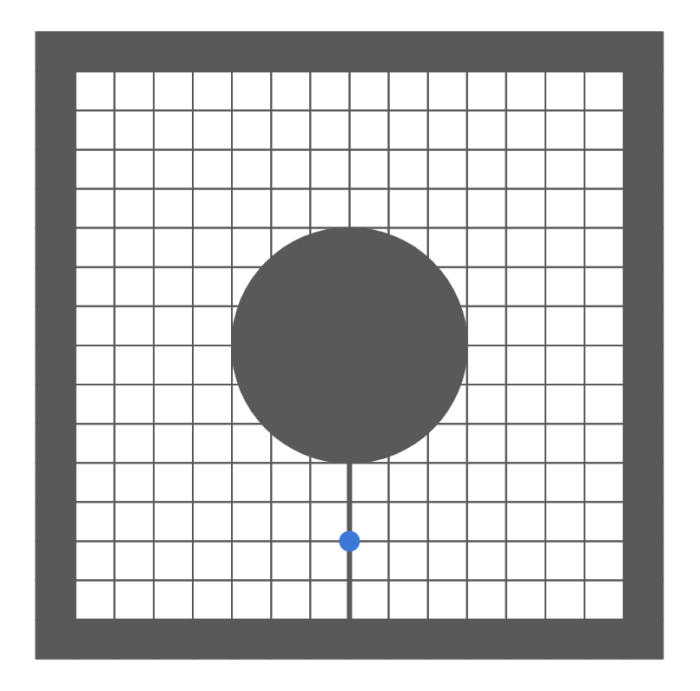
Each move takes one second. For your first move, you can choose among nine grid points surrounding and including the starting position.

From there, it’s essential to remember that you have inertia. So for your second move, you again have nine possible destinations, but they are determined by your current velocity vector. That is, you can maintain your current direction and speed, or you can alter your destination by one point in any direction (horizontally, vertically or diagonally). For example, if your first move was up and to the right, then your possible second moves are shown below, although two of them will cause you to crash into the wall.

So how quickly can you navigate the following track? Fractional times are allowed, so if the finish line bisects your final move, then that move counts as 0.5 seconds toward your total time. And remember, at no time can your path venture into the wall. (Being tangent to the wall is allowed, as is being on a grid point along a wall.)

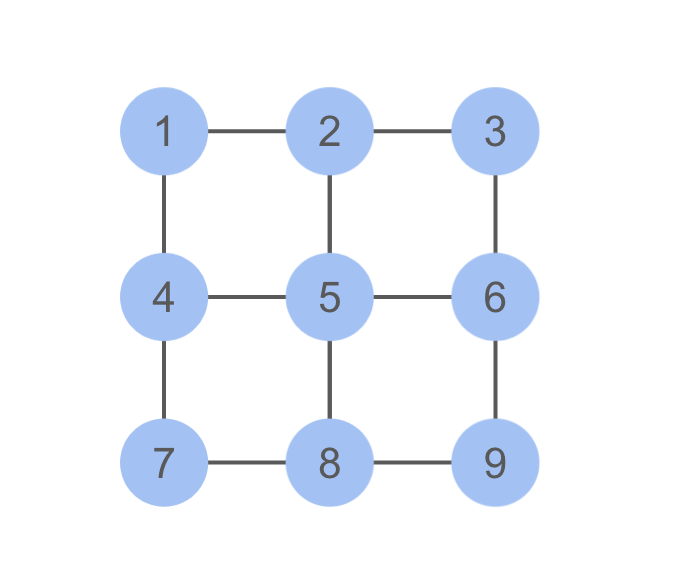
Finally, submitting your answer can be tricky work. Please be sure to submit both your total time, as well as your sequence of moves. Each move should be assigned a digit from 1 through 9, corresponding to the nine possible destinations of the move:

Your overall path around the course then corresponds to a unique sequence of digits.

Do you have what it takes to win the Riddler-opolis 500? Puzzle enthusiasts, start your engines!

Answer

I determined many solutions that ended in 12-13 seconds. 12 seems difficult to break, as 3 seconds per quarter circle is difficult to decrease. If one does decrease it, there is too much inertia, and the velocity and direction would either crash into a wall or add too many additional seconds to slow down and turn.

Two examples are:

$3-6-1-4-4-7-8-9-8-9-3-3$ and $6-3-1-1-7-7-8-9-8-6-6-3$

Rohan Lewis

2021.08.09