Can You Build The Wall?

Riddler Classic

Today marks the beginning of the Summer Olympics! One of the brand-new events this year is sport climbing, in which competitors try their hands (and feet) at lead climbing, speed climbing and bouldering.

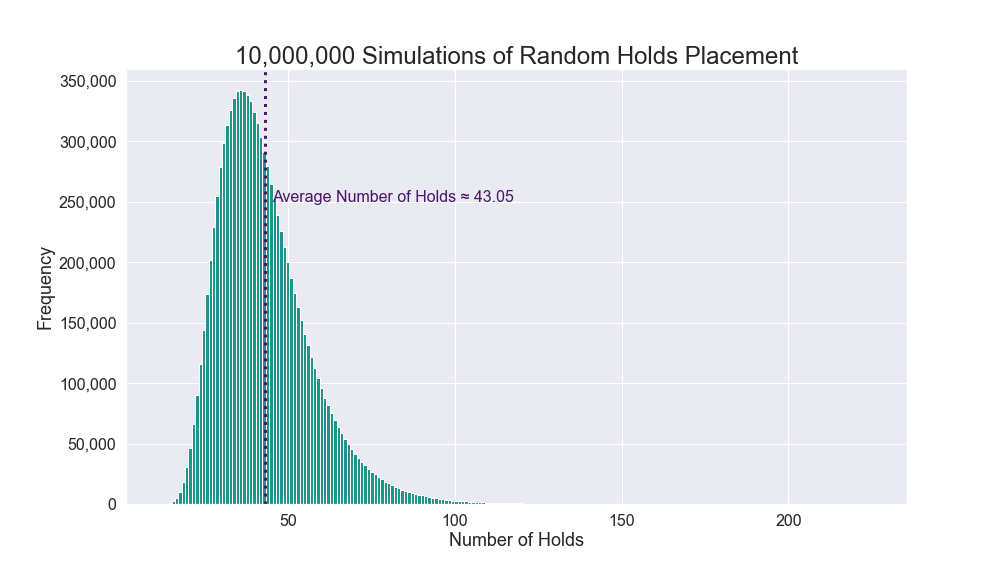
Suppose the event’s organizers accidentally forgot to place all the climbing holds on and had to do it last-minute for their 10-meter wall (the regulation height for the purposes of this riddle). Climbers won’t have any trouble moving horizontally along the wall. However, climbers can’t move between holds that are more than 1 meter apart vertically.

In a rush, the organizers place climbing holds randomly until there are no vertical gaps between climbing holds (including the bottom and top of the wall). Once they are done placing the holds, how many will there be on average (not including the bottom and top of the wall)?

Extra credit: Now suppose climbers find it just as difficult to move horizontally as vertically, meaning they can’t move between any two holds that are more than 1 meter apart in any direction. Suppose also that the climbing wall is a 10-by-10 meter square. If the organizers again place the holds randomly, how many have to be placed on average until it’s possible to climb the wall?

Solution

Using code, I ran the following:

• Create a wall with holds at 0 and 10
• Add a random hold between 0 and 10.
• For all consecutive holds, subtract the distances, create a list of differences.
• If the maximum of the differences is greater than 1, add another hold and repeat the above step.
• If the maximum of the differences is less than or equal to 1, return the number of holds, not including 0 or 10.

Answer

Rohan Lewis

2021.07.25

Code can be found here.