Answer¶
On June 24, the following challenge was posted on Twitter:
In this challenge, the numbers from 1 to 11 are arranged in a circle in a particular order: 1, 4, 8, 7, 11, 2, 5, 9, 3, 6, 10. You then have to connect pairs of numbers with straight line segments that don’t intersect, and your score is the sum of the products of the joined numbers. For example, with the connections {1, 4}, {8, 10}, {3, 7}, {5, 9}, and {2, 11} (and the 6 left by itself), you get a score of 1·4 + 8·10 + 3·7 + 5·9 + 2·11, or 172.
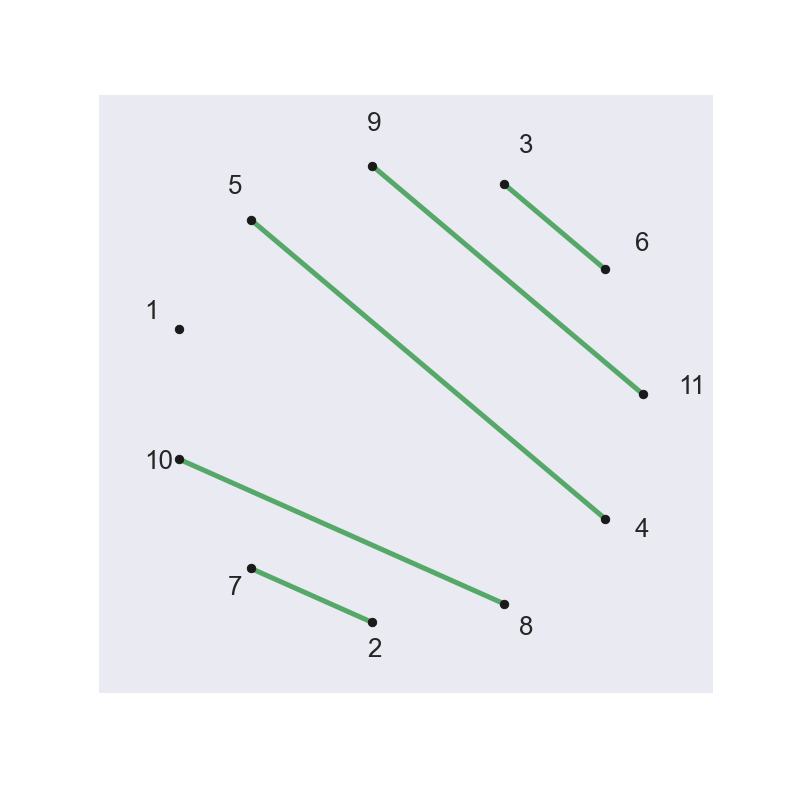
The best score you can achieve with this ordering of 1 through 11 around the circle is 237, which you can get with the following connections: {6, 10}, {3, 4}, {7, 8}, {9, 11} and {2, 5} (and the 1 left by itself).
This got Friend-of-The-Riddler Tyler Barron and me thinking about possible extensions of this challenge. If you want the highest possible maximum score, then you can rearrange the numbers from 1 to 11 so that they are in numerical order around the circle. (With this arrangement, the maximum score is 250.)
But what if you want the lowest possible maximum score? That is, how can you order the numbers from 1 to 11 around the circle so that the maximum possible score is as low as possible? And what is the resulting score?
Note that looking only at 8, 9, 10, and 11 yield 178 to 182. Looking at only 6, 7, 8, 9, 10, and 11 yield 208 to 224.
Using this, I estimated the answer will be fairly close to 237.
I came up the following scenario based around the above statements, by strategically placing numbers between the largest.
231 is the lowest maximum I could find.
