Can You Maximize Your Solitaire Winnings?

Riddler Classic

This week’s Classic comes from Henk Tijms, author of Basic Probability, What Every Math Student Should Know.

Riddler solitaire is played with 11 cards: an ace, a two, a three, a four, a five, a six, a seven, an eight, a nine, a 10 and a joker. Each card is worth its face value in points, while the ace counts for 1 point. To play a game, you shuffle the cards so they are randomly ordered, and then turn them over one by one. You start with 0 points, and as you flip over each card your score increases by that card’s points — as long as the joker hasn’t shown up. The moment the joker appears, the game is over and your score is 0. The key is that you can stop any moment and walk away with a nonzero score.

What strategy maximizes your expected number of points?

Extra credit: With an optimal strategy, how many points would you earn on average in a game of Riddler solitaire?

Solution

Consider a more general deck of $n$ cards, with an ace, numbers from $2$ to $n-1$, and a joker. As described, each card is worth its face value and the ace is $1$ point. For the sake of calculations and casework, let us assume that cards are still flipped after the joker, but the sum remains $0$.

The sum of all non-joker cards is $\dfrac{n(n-1)}{2}$.

Here are some select expected values after flipping the $k^{th}$ card.

$k = 0$

You are expected to get 0 points.

$k = 1$

There are $n-1$ non-joker cards flipped card scenarios of $1$ card each. The expected value is thus:
$$\dfrac{1}{n} \cdot \dfrac{n(n-1)}{2} = \dfrac{n-1}{2}$$

$k = n-1$

There are $(n-1)!$ non-joker flipped card scenarios of $n-1$ cards each. Each card appears exactly:
$$(n-1)! \cdot \dfrac{n-1}{n-1} = (n-1)!$$
times, or exactly once in every scenario. Including the joker, there are $n!$ flipped card scenarios. The expected value is thus:
$$\dfrac{(n-1)! \cdot \dfrac{n(n-1)}{2}}{n!} = \dfrac{n-1}{2}$$

$k = n$

All cards have been flipped, including the joker. You are expected to get 0 points.

The above cases seem symmetric, perhaps even a quadratic relationship.

Any $k$

There are $\dfrac{(n-1)!}{(n-1-k)!}$ non-joker flipped card scenarios of $k$ cards each. Each non-joker card appears exactly:
$$\dfrac{(n-1)!}{(n-1-k)!} \cdot \dfrac{k}{n-1} = \dfrac{k \cdot (n-2)!}{(n-1-k)!}$$
times. Including the joker, there are $\dfrac{n!}{(n-k)!}$ flipped card scenarios. The expected value is thus:
$$\dfrac{\dfrac{k \cdot (n-2)!}{(n-1-k)!} \cdot \dfrac{n(n-1)}{2}}{\dfrac{n!}{(n-k)!}}$$
$$ = \dfrac{k \cdot n!}{2 \cdot (n-1-k)!} \cdot \dfrac{(n-k)!}{n!}$$
$$ = \dfrac{k \cdot (n-k)}{2}$$

n = 3

Note that for $n = 3$, $k = 1$ or $2$ yield an expected value of $1$.

However, a larger expected value can be achieved.

First card is $0$

Two of the six possibilities yield $0$ points.

First card is $1$

Two of the six possibilities yield $1$ points.

It is advantageous to go for the second card in this situation, as one possibility will yield $0$ points and one will yield $3$ points.

First card is $2$

Two of the six possibilities yield $2$ points.

Expected Value

The maximum expected value is thus $\dfrac{7}{6}$.

Note that the increase in expected value is because the additional $2$ is greater than the $1$ that is removed.

Answer

Assume $k$ cards have been flipped up (that have sum $p$), leaving $n-k$ to be seen $\left( \text{of sum }q = \dfrac{n(n-1)}{2} - p \right)$.

The expected value added to the sum $p$ for the next flipped card is $\dfrac{q - p}{n-k}$.

Therefore, if the sum of the remaining cards is greater than the flipped cards, one should continue playing.

And likewise, if the sum of the cards flipped up is greater than or equal to the sum of the cards remaining, one should stop playing!

Extra Credit

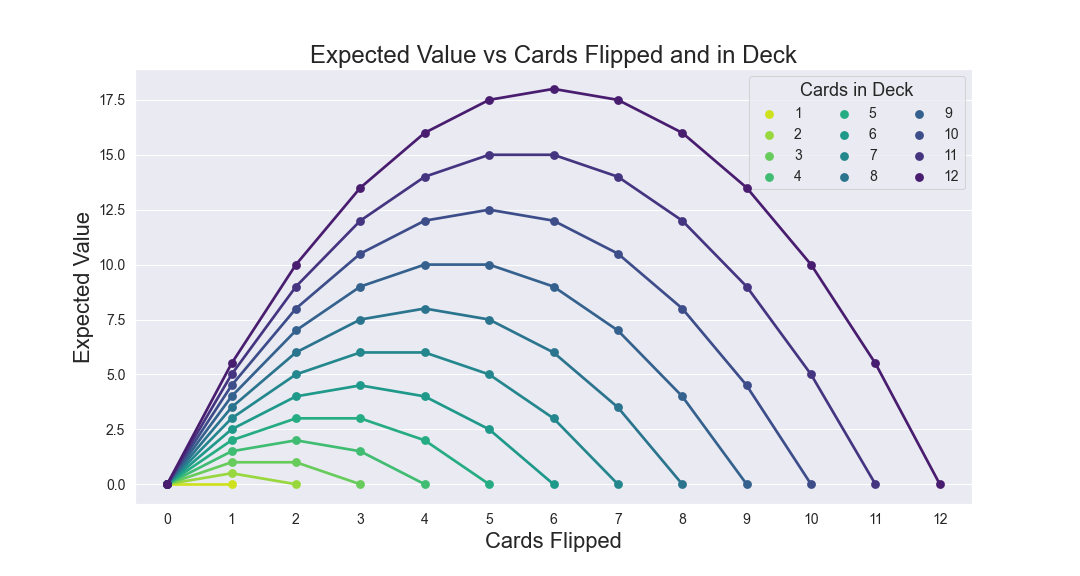
My equation for expected value is a lower limit. However, I did calculate some smaller deck values.

(Update 2021.06.29...I created an algorithm and achieved answers for n = 7, 8, 9, 10, 11)

Deck Size	$k$	Lower Limit : $\dfrac{k \cdot (n-k)}{2}$	Maximum Expected Value
$2$	$1$	$\dfrac{1}{2}$	$\dfrac{1}{2}$
$3$	$1$ or $2$	$1$	$\dfrac{7}{6}$
$4$	$2$	$2$	$\dfrac{48}{24} = 2$
$5$	$2$ or $3$	$3$	$\dfrac{384}{120} = 3.2$
$6$	$3$	$4.5$	$\dfrac{3336}{720} \approx 4.63$
$7$	$3$ or $4$	$6$	$\dfrac{31704}{5040} \approx 6.29$
$8$	$4$	$8$	$\dfrac{330624}{40320} \approx 8.2$
$9$	$4$ or $5$	$10$	$\dfrac{3761856}{362880} \approx 10.37$
$10$	$5$	$12.5$	$\dfrac{46402560}{3628800} \approx 12.79$
$11$	$5$ or $6$	$15$	computing

My guess is for $n=11$, the maximum expected value will be slightly greater than the $15$ achieved from $k=5$ or $6$.

(Update 2021.06.29...it seems that I may be pretty close.)

Rohan Lewis

2021.06.28 (Updated 2021.06.29)

Code can be found here.