Can You Count The Crashes?

Riddler Classic

From Ben Edelstein comes a crash course in probability:

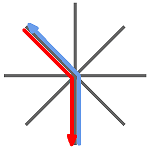
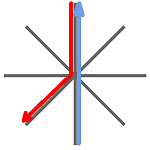
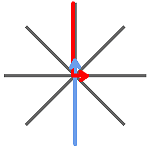
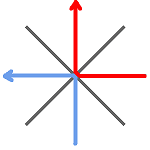
Eight two-way roads all converge at a single intersection, as shown in the diagram below.

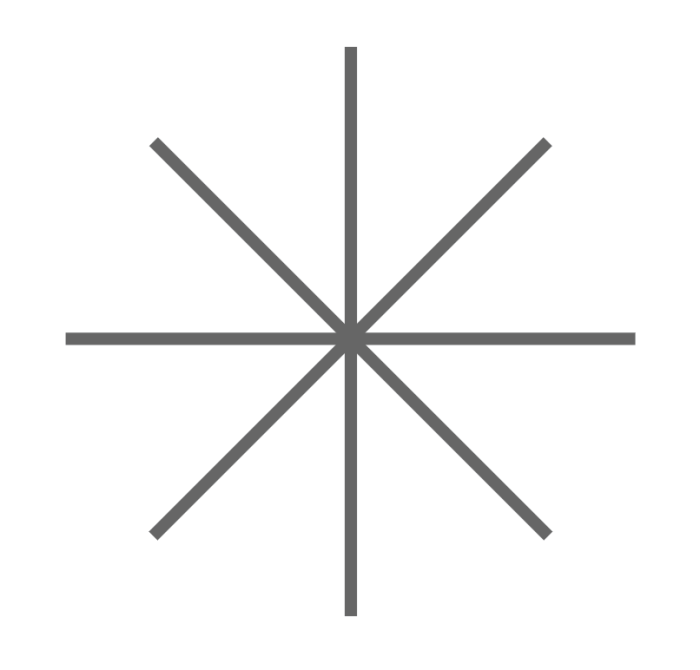
Two cars are heading toward the single intersection from different directions chosen at random. Upon reaching the intersection, they both turn in a random direction (where proceeding straight is a possible “turn”) — however, neither car pulls a U-turn (i.e., heads back the way it came).

In some cases, the paths of the cars can be drawn so that they do not cross. In this case, all is well.

However, in other cases, the paths must cross. In this event, the cars will crash.

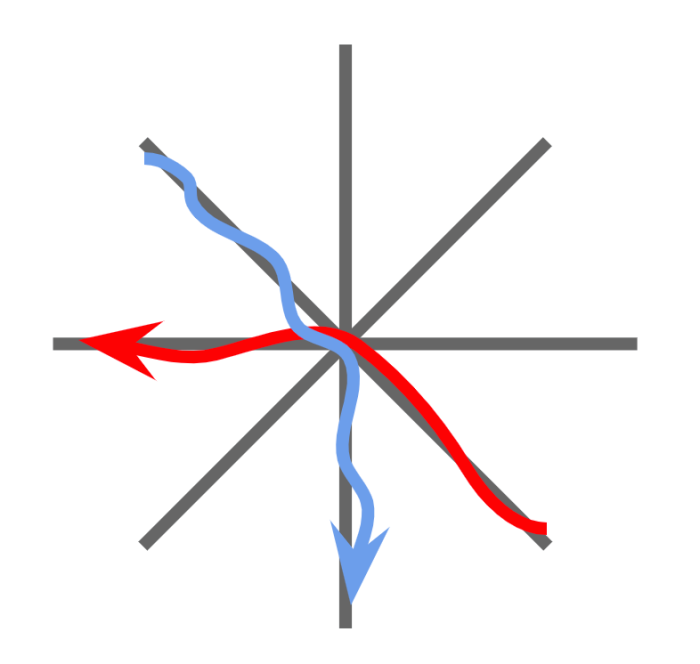
What is the probability the cars will crash? (If both cars head off in the same direction, that also counts as a crash.)

Extra credit: As the number of two-way roads converging at the intersection approaches infinity, what value does the probability of crashing approach?

Solution

For $n$ roads two-way roads converging at an intersection, there are $n \choose 2$ ways for the initial locations of the two cars. From their perspective, they can each end up at any of the remaining $n-1$ roads.

Thus there are a total of $\dfrac{n(n-1)^3}{2}$ scenarios.

There are 3 cases and 8 subcases that exemplify the paths of the two cars, relative to each other.

Number of Roads	Description	Crash?	Example	How to Calculate	Calculation
2	The start and end road of one car is the respective end road and start road of the other car.	Non-Crash		Chose any two roads.	${n \choose 2} = \dfrac{n(n-1)}{2}$
3	The cars start on different roads, but crash on the same end road.	Crash		Chose any road as the common road and two roads from the remaining.	$n \cdot {{n-1} \choose 2} =$ $\dfrac{n(n-1)(n-2)}{2}$
3	One car's end road is the same as the other car's start road. The car paths are always on the left of each other.	Non-Crash		Chose any road as the common road and two roads from the remaining.	$n \cdot {{n-1} \choose 2} =$ $\dfrac{n(n-1)(n-2)}{2}$
3	One car's end road would be the other car's start road, but they crash.	Crash		Chose any road as the common road and two roads from the remaining.	$n \cdot {{n-1} \choose 2} =$ $\dfrac{n(n-1)(n-2)}{2}$
4	One car path is always on the right of the other car path, and one car path is always on the left of the other car path.	Non-Crash		Chose four roads and the pattern can be rotated four ways.	$4 \cdot {n \choose 4} =$ $\dfrac{n(n-1)(n-2)(n-3)}{6}$
4	Both car paths are always on the right of the other car path.	Non-Crash		Chose four roads and the pattern can be rotated only two ways.	$2 \cdot {n \choose 4} =$ $\dfrac{n(n-1)(n-2)(n-3)}{12}$
4	Both car paths are always on the left of the other car path.	Non-Crash		Chose four roads and the pattern can be rotated only two ways.	$2 \cdot {n \choose 4} =$ $\dfrac{n(n-1)(n-2)(n-3)}{12}$
4	The cars start on different roads and are heading towards different roads, but crash.	Crash		Chose four roads and the pattern can be rotated four ways.	$4 \cdot {n \choose 4} =$ $\dfrac{n(n-1)(n-2)(n-3)}{6}$

Sum of Cases:

$$\dfrac{n(n-1)}{2} + 3\left(\dfrac{n(n-1)(n-2)}{2}\right) + 2\left(\dfrac{n(n-1)(n-2)(n-3)}{6}\right) + 2\left(\dfrac{n(n-1)(n-2)(n-3)}{12}\right)$$

$$= \dfrac{n(n-1)}{2} + \dfrac{3n(n-1)(n-2)}{2} + \dfrac{3n(n-1)(n-2)(n-3)}{6}$$

$$= \dfrac{n(n-1)}{2}\left(1 + 3(n-2) + (n-2)(n-3)\right)$$

$$= \dfrac{n(n-1)}{2}\left(1 + (n-2)(3+n-3)\right)$$

$$= \dfrac{n(n-1)}{2}(n^2-2n+1)$$

$$= \dfrac{n(n-1)^3}{2}$$

Since this checks, I shall proceed with crashes and non-crashes.

Sum of Crashes:

$$2\left(\dfrac{n(n-1)(n-2)}{2}\right) + \left(\dfrac{n(n-1)(n-2)(n-3)}{6}\right)$$

$$= n(n-1)(n-2)\left(1 + \dfrac{n-3}{6}\right)$$

$$= \dfrac{n(n-1)(n-2)(n+3)}{6}$$

Sum of Non-Crashes:

$$\dfrac{n(n-1)}{2} + \dfrac{n(n-1)(n-2)}{2} + \dfrac{n(n-1)(n-2)(n-3)}{6} + 2\left(\dfrac{n(n-1)(n-2)(n-3)}{12}\right)$$

$$= \dfrac{n(n-1)}{2} + \dfrac{n(n-1)(n-2)}{2} + \dfrac{n(n-1)(n-2)(n-3)}{3}$$

$$= \dfrac{n(n-1)}{6}\left(3 + 3(n-2) + 2(n-2)(n-3)\right)$$

$$= \dfrac{n(n-1)}{6}\left(3 + (n-2)(3 + 2(n-3))\right)$$

$$= \dfrac{n(n-1)}{6}\left(3 + (n-2)(2n-3)\right)$$

$$= \dfrac{n(n-1)(2n^2-7n+9)}{6}$$

Answer

The probability of a crash can thus be expressed as:

$$\dfrac{\dfrac{n(n-1)(n-2)(n+3)}{6}}{\dfrac{n(n-1)^3}{2}}$$

$$ = \dfrac{(n-2)(n+3)}{3(n-1)^2}$$

For $8$ roads, this is:

$$\dfrac{(6)(11)}{3(7)^2} = \dfrac{22}{49} \approx 44.90\%$$

Extra Credit

For the number of roads approaching infinity,

$$\lim_{n\to\infty} {\dfrac{(n-2)(n+3)}{3(n-1)^2}} $$

$$ = \lim_{n\to\infty} {\dfrac{(1-\frac{2}{n})(1+\frac{3}{n})}{3(1-\frac{1}{n})^2}}$$

$$= \dfrac{1}{3}$$

Rohan Lewis

2021.06.20