Dakota Jones is back in action! To gain access to a hidden temple deep in the Riddlerian Jungle, she needs a crystal key.
She already knows the crystal is a polyhedron. And according to an ancient text, it has exactly six edges, five of which are 1 inch long. Cryptically, the text does not specify the length of the sixth edge. Instead, it says that the key is the largest such polyhedron (i.e., with six edges, five of which have length 1) by volume.
Once again, Dakota Jones needs your help. What is the volume of the crystal key?
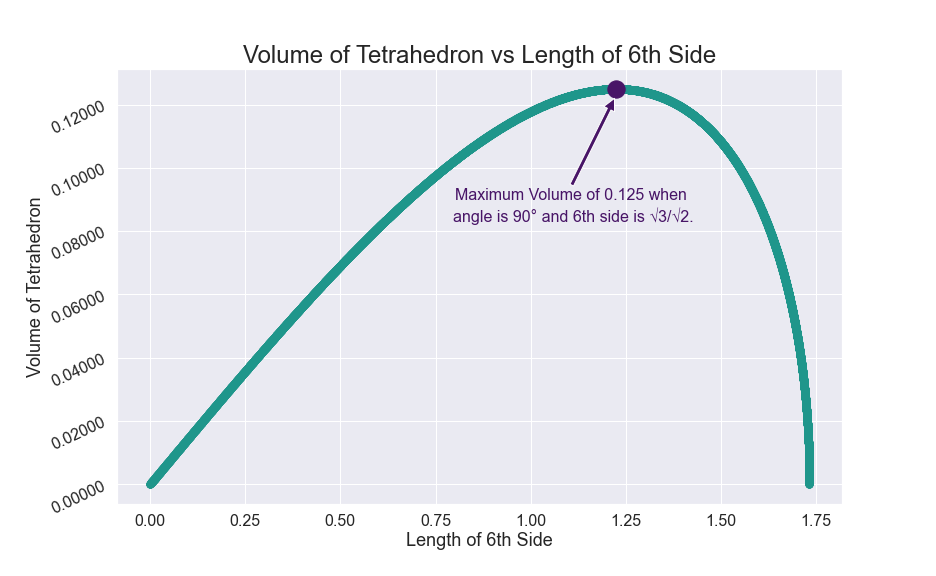
Given the description of the tetrahedron, think of it as two equilateral triangles hinging upon a shared edge. The remaining edge length varies from $0$, where the two equilateral triangles are the same, to $\sqrt{3}$, where the two equilateral triangles make a $180^{\circ}$ angle with each other.
The volume of a Tetrahedron can be determined from all 6 sides in a Heron-type formula.
Let $U$ be the variable side, and $V = W = u = v = w = 1$.
It follows that, $X = 4 - U^2$, $Y = Z = 3$, $x = U^2$, and $y = z = 1$.
It follows that, $p = 3U$, $q = r = \sqrt{12-3U^2}$, and $s = U$.
It follows that,
$$V = \frac{\sqrt{\left(2\sqrt{12-3U^2}-2U\right) \cdot (4U) \cdot (4U) \cdot \left(2\sqrt{12-3U^2}+2U\right)}}{192uvw}$$
$$= \frac{8U\sqrt{\left(\sqrt{12-3U^2}-U\right) \cdot \left(\sqrt{12-3U^2}+U\right)}}{192}$$
$$= \frac{8U\sqrt{\left(12-3U^2-U^2\right)}}{192}$$
$$= \frac{16U\sqrt{\left(3-U^2\right)}}{192} = \frac{U\sqrt{\left(3-U^2\right)}}{12}$$
Solving for $V' = 0$
$$0 = \dfrac{1}{12} \cdot \left(U \cdot \frac{1}{2}\frac{-2U}{\sqrt{3-U^2}} + 1 \cdot \sqrt{3-U^2} \right)$$
$$= \left(\frac{-U^2 + 3 - U^2}{\sqrt{3-U^2}} \right) = \frac{3 - 2U^2}{\sqrt{3-U^2}}$$
Maximum Volume occurs at $U = \dfrac{\sqrt{3}}{\sqrt{2}}$,
$$V_{max} = \frac{\dfrac{\sqrt{3}}{\sqrt{2}}\sqrt{\left(3-\left(\dfrac{\sqrt{3}}{\sqrt{2}}\right)^2\right)}}{12}$$$$= \frac{\dfrac{\sqrt{3}}{\sqrt{2}}\sqrt{\dfrac{3}{2}}}{12}= \dfrac{1}{8}$$
The video below animates varying lengths of the 6th side.