No Isosceles Triangles For You!¶
Riddler Classic¶
This week’s Classic is being served up by Jordan Ellenberg, whose new book, “Shape,” goes on sale on May 25.
One of the many geometers who appears in “Shape” is the great Paul Erdős. In 1946, Erdős himself posed a riddle about what are called “isosceles sets”: How many points can you place in d-dimensional space such that any three of them form an isosceles triangle?
In two dimensions, the largest isosceles set has exactly six points, with five forming the vertices of a regular pentagon and the sixth point in the middle. In three dimensions, the largest isosceles set has eight points; in four dimensions, the largest set has 11 points. And in dimensions higher than eight, no one knows what the largest isosceles sets might be!
But this week, Jordan is asking about what he calls anti-isosceles sets. Consider a $N×N$ grid of points. What is the greatest subset of these $N^2$ points such that no three of them form an isosceles triangle? (Note: Degenerate triangles, or triangles with zero area, do count as triangles here, as long as their three vertices are distinct.)
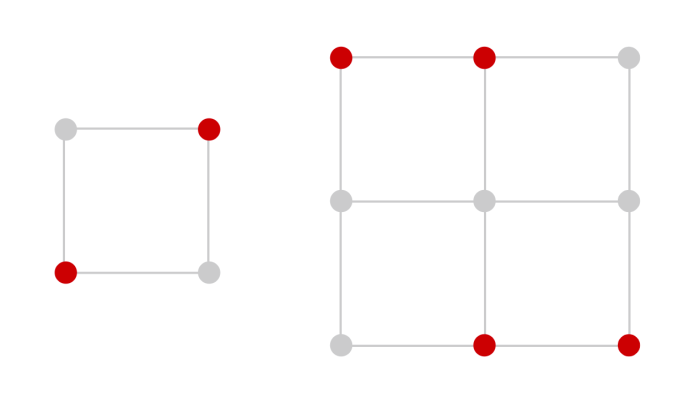
As shown below, the largest anti-isosceles set in a 2×2 grid has two points; for a 3×3 grid, the largest anti-isosceles set has four points. (Note: For both grids, there are multiple sets with these maximum numbers of points.)
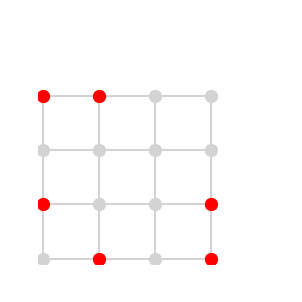
How many points are in the largest anti-isosceles set for a 4×4 grid?
Extra credit: What about a $5×5$ grid, a $6×6$ grid, or even larger square grids? Can you find an expression (or bounds) for the size of the largest anti-isosceles set for the general $N×N$ grid? (If you figure out anything about the general case, Jordan would love to hear about it!)