Can You Cut The Perfect Pancake?¶
Riddler Express¶
After you intended to make a perfectly circular pancake, the batter has spread out, filling every last corner of your square pan. (It is unclear why you were using a square pan in the first place.)
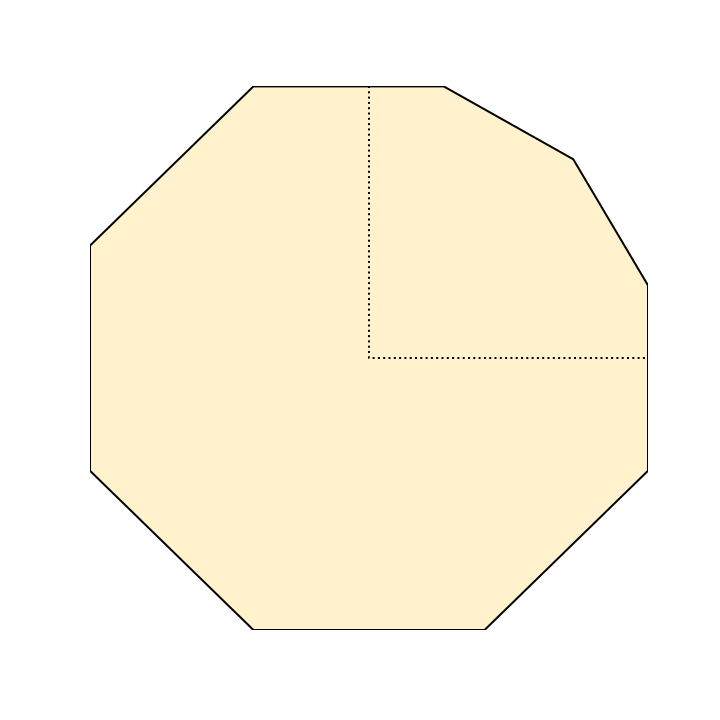
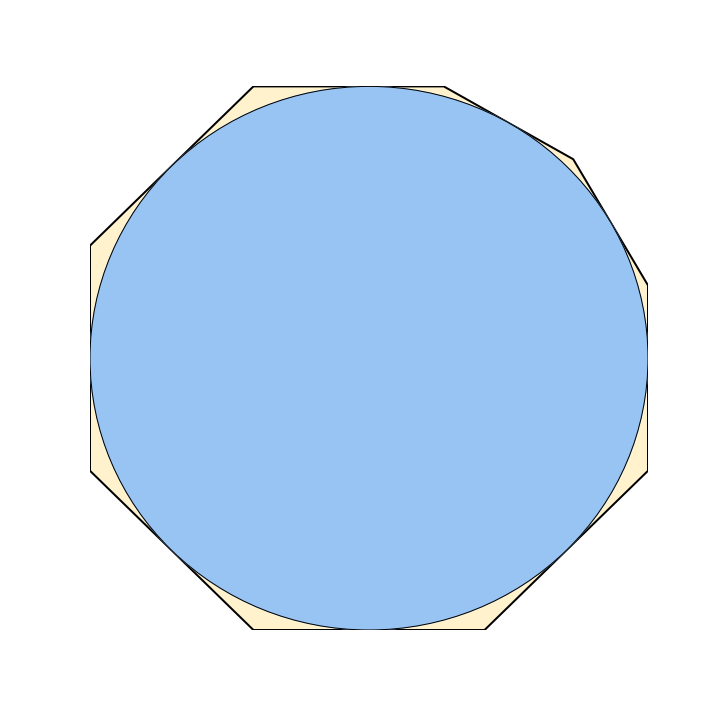
To salvage your breakfast, you plan to slice off the corners of your square pancake, giving you something closer to a circle. The image below shows one such slice you might make. Each slice must be straight, and no slice can pass through the inscribed blue circle that represents your original desired pancake.

Of course, there’s a catch. You can make at most five slices. If the blue circle has a radius of 1 unit, what is the minimum possible area your pancake can have after five slices?
(Kudos to anyone who actually constructs an edible pancake with this minimum area.)