Can You Crack The Case Of The Crescent Moon?

Riddler Classic

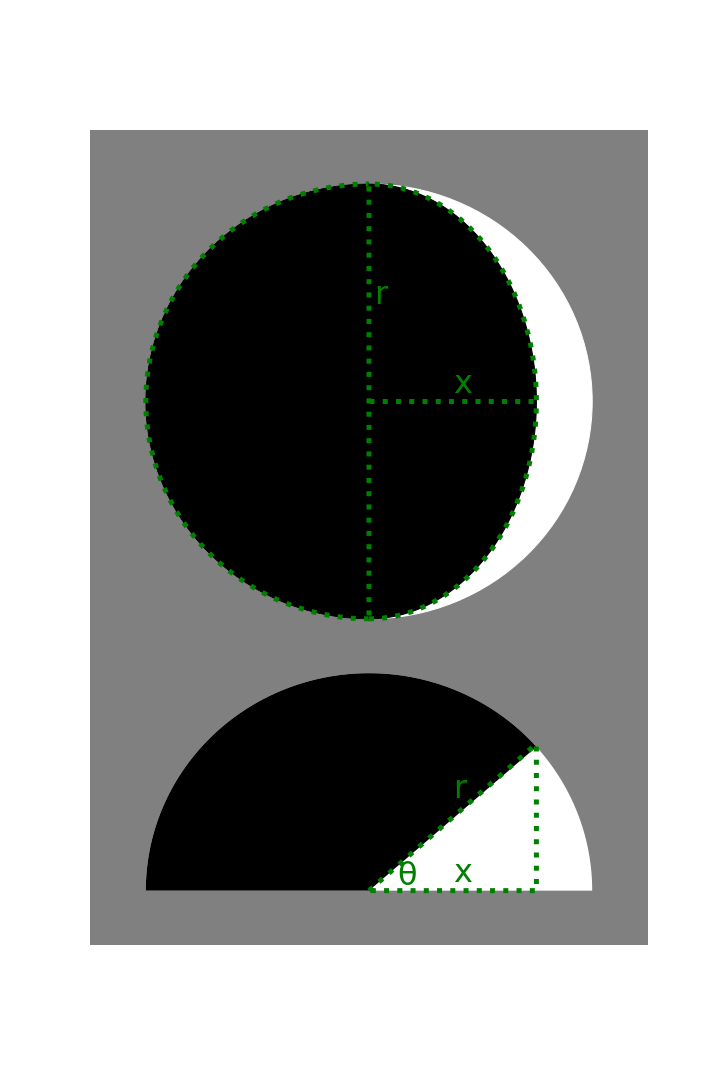
This past Monday marked the beginning of Ramadan in the U.S. The month-long observance traditionally begins with the sighting of a crescent moon, or hilal, after a new moon. For this week’s Classic, let’s take a closer look at a waxing crescent moon.

After a new moon, the crescent appears to grow slowly at first. At some point, the moon will be one-sixth full by area, then one-quarter full, and so on. Eventually, it becomes a half-moon, at which point its growth begins to slow down. The animation below provides some insight into what’s happening here:

How many times faster is the area of the illuminated moon growing when it is a half-moon versus a one-sixth moon?

(Some simplifying assumptions you might make for this problem are that the moon is a perfect sphere, that its orbit around Earth is a perfect circle, that the moon orbits the Earth much faster than the Earth orbits the sun and that the sun is very, very far away. If you make additional assumptions, feel free to include them in your response.)

Solution

The assumption I am making is that the boundary of illumination/shadow across the surface of the moon rotates as a circle through the poles at a constant rate.

The illuminated area of the moon is a semicircle plus (or minus) the area of a semi ellipse. The diagram below illustrates the view from the front and bottom.

The triangle from the bottom view yields $x = r \cos \theta$.

Since the illuminated area can be calculated as a semicircle $±$ semi ellipse,

$$A = \frac{\pi r^2}{2} - \frac{\pi r^2\cos \theta}{2}$$

$$= \frac{\pi r^2}{2} \left(1 - \cos \theta\right)$$

The rate of change of area can be calculated as,

$$\frac{dA}{dt} = \frac{\pi r^2}{2} \left(\sin \theta\right)\frac{d \theta}{dt} = k \left(\sin \theta\right)$$

Half-Moon

$$A_{\frac{1}{2}} = \frac{\pi r^2}{2} = \frac{\pi r^2}{2} \left(1 - \cos \theta\right)$$

$$0 = \cos \theta$$
$$\theta = \frac{\pi}{2}$$
It follows that $$\frac{dA_{\frac{1}{2}}}{dt} = k \left(\sin \frac{\pi}{2} \right) = k$$

One-Sixth Moon

$$A_{\frac{1}{6}} = \frac{\pi r^2}{6} = \frac{\pi r^2}{2} \left(1 - \cos \theta\right)$$

$$\frac{1}{3} = \left(1 - \cos \theta\right)$$
$$\cos \theta = \frac{2}{3}$$
Applying $\cos^2 \theta + \sin^2 \theta = 1$ yields $\sin \theta = \frac{\sqrt{5}}{3}$.

It follows that $$\frac{dA_{\frac{1}{6}}}{dt} = \frac{k\sqrt{5}}{3}$$

Answer

$$\frac{\frac{dA_{\frac{1}{2}}}{dt}}{\frac{dA_{\frac{1}{6}}}{dt}} = \frac{k}{\frac{k\sqrt{5}}{3}}= \frac{3}{\sqrt{5}} \approx 1.342$$

The half moon illuminated area is increasing approximately $1.342$ times faster than that of the one-sixth moon.

Rohan Lewis

2021.04.19

Code can be found here.