Can You Navigate the One-Way Streets?

Riddler Classic

From Graydon Snider comes a one-way trip to a tangle of grids:

In Riddler City, all the streets are currently two-way streets. But in an effort to make the metropolis friendlier for pedestrians and cyclists, the mayor has decreed that all streets should be one-way. Meanwhile, the civil engineer overseeing this transition is not particularly invested in the project and will be randomly assigning every block of each street a random direction.

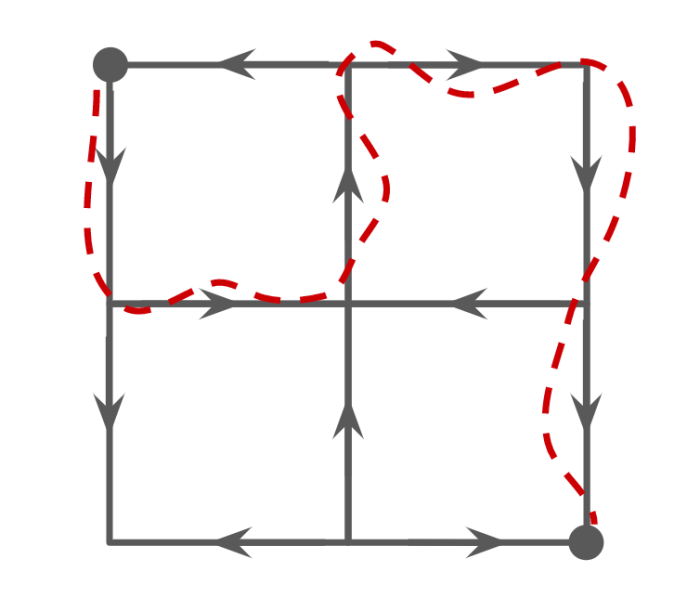
For your daily commute to work, you drive a car two blocks east and two blocks south, as shown in the diagram below. What is the probability that, after each block is randomly assigned a one-way direction, there will still be a way for you to commute to work while staying within this two-by-two block region (i.e., sticking to the 12 streets you see in the diagram)? Here is one such arrangement of one-way streets that lets you commute to work:

And no, you can’t get out of your car to hop on a bike or walk. I mean, you can, but not in this puzzle.

Solution

There are $2^{12} = 4,096$ total block configurations.

There are $3$ categories and $14$ subcategories of block configurations that lead to work.

Routes of length $= 4$

Routes of length $= 6$

Routes of length $= 8$

Answer

While it easy to count the total number for each subcatgory, counting all block configurations becomes difficult with overlapping block configurations. Using code, I arrived at

$$\dfrac{1135}{4096} \approx 27.71\%$$

General Solution

I briefly explored a one-by-one block region and a one-by-two block region as well. The probability of arriving at any location, starting from the top left, using the same random assignment of block directions, is shown below.

1x1

1x2

No clear pattern emerges, and I am more confused. :(

Rohan Lewis

2021.04.12

Code can be found here.