Can You Solve for the Squares?¶

Riddler Express ¶

Many of you already know of Catriona Agg’s delightful felt-tip geometric puzzles (or as I like to call them, “Agg-onizers”). This past week, I reached out to her to let her know I planned to run a puzzle inspired by her brainteasers, and wouldn’t you know it — she offered to create a felt-tip drawing just for Riddler Nation!

Without further ado, I present a puzzle that has been hand-drawn by Catriona:

The two larger squares are congruent, and the smaller square makes a 45 degree angle with one of the larger squares. Both larger squares touch the circle at one corner, while the smaller square touches the circle at two corners.

How many times greater is the area of one of the larger squares than the area of the smaller square?

Solution¶

Looking at the top half of the puzzle, draw a vertical in the center. Because of symmetry and the equivalent sides, the following variables have been applied to the squares:

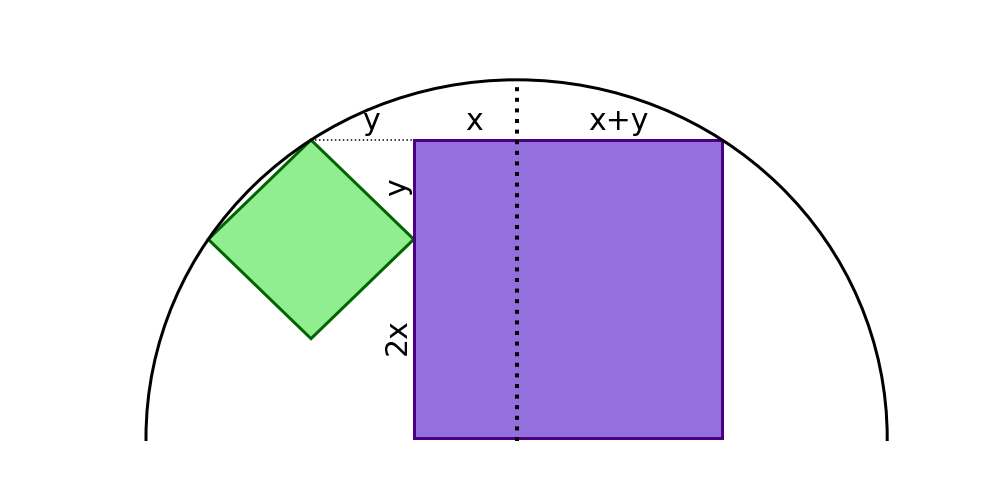
The radius of the circle can be determined from:

The radius of the circle can also be determined from:

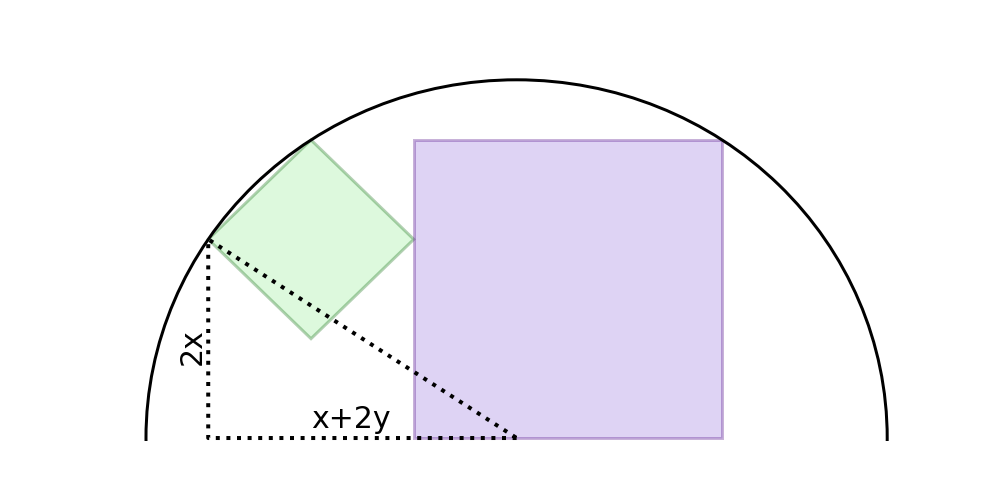
Setting the two equal,

$$\left(2x+y\right)^2 + \left(x+y\right)^2 = \left(2x\right)^2 + \left(x+2y\right)^2$$

$$\left(4x^2 + 4xy + y^2\right) + \left(x^2+2xy+y^2\right) = \left(4x^2\right) + \left(x^2+4xy+4y^2\right)$$
$$5x^2 + 6xy + 2y^2 = 5x^2+4xy+4y^2$$
$$2xy = 2y^2$$
$$x = y$$

Answer¶

The area of the small square is $2x^2$. The area of the large square is $9x^2$. The large square is therefore $4.5$ times larger than the small square.

Rohan Lewis¶

2021.03.22¶