Answer¶
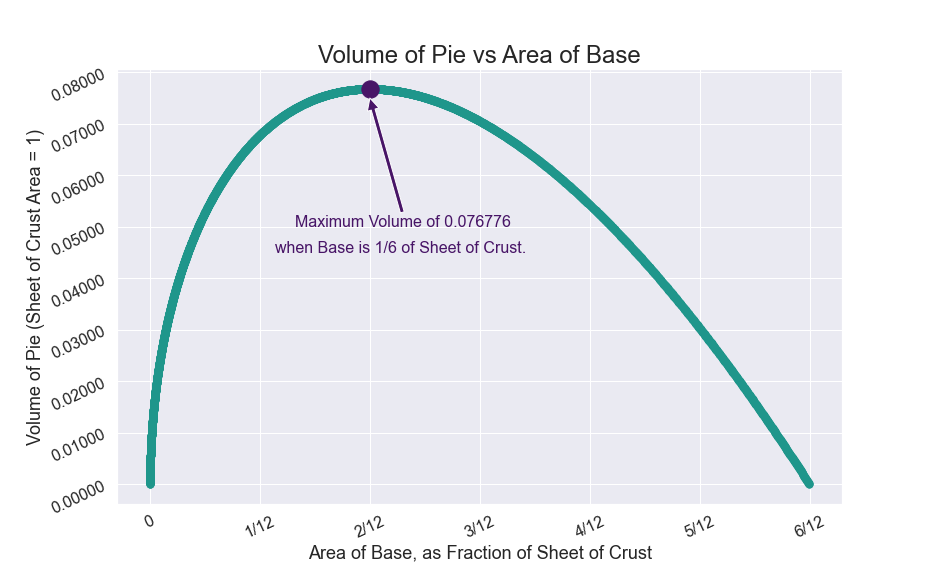
The circular base should be $\dfrac{1}{6}$ of the sheet of crust to achieve maximum pie volume. 😋😋
The video below animates the pies.
This Sunday, March 14, is Pi Day! To celebrate, you are planning to bake a pie. You have a sheet of crust laid out in front of you. After baking, your pie crust will be a cylinder of uniform thickness (or rather, thinness) with delicious filling inside.
To maximize the volume of your pie, what fraction of your crust should you use to make the circular base (i.e., the bottom) of the pie?
Note: If you solve this riddle by baking an optimal pie, you automatically win.
The area of a cylinder is
$$A = 2 \pi r^2 + 2 \pi rh$$Substituting $B = \pi r^2$ yields
$$A = 2B + 2 \sqrt{\pi B} h$$
$$ => 2 \sqrt{\pi B} h = A - 2B$$
$$ => h = \frac{A - 2B}{2 \sqrt{\pi B}}$$
Substituting for h in $V = Bh$,
$$ = \frac{1}{2 \sqrt{\pi}} \cdot \left(A\sqrt{B} - 2B\sqrt{B}\right)$$
In order to maximize volume, set $\dfrac{dV}{dB} = 0$:
$$ => 0 = \frac{1}{2 \sqrt{\pi}} \cdot \left(\frac{A}{2\sqrt{B}} - 2\cdot \frac{3}{2}\sqrt{B}\right)$$
$$ = \frac{1}{4 \sqrt{\pi B}} \cdot \left(A - 6B\right)$$
$$ => B = \frac{A}{6}$$

The circular base should be $\dfrac{1}{6}$ of the sheet of crust to achieve maximum pie volume. 😋😋
The video below animates the pies.