Can You Bat .299 in 299 Games?¶
On Feb. 23, baseball statistician Jim Passon tweeted out some recent stats for baseball’s God of WAR, Mike Trout:
Yes, Trout’s numbers are gaudy. But what caught social media’s attention was that each stat (batting average, on-base percentage, slugging percentage and OPS) somehow had a corresponding number of games over which Trout averaged those stats. For example, Trout batted .299 over his last 299 games. Could this possibly be a coincidence?
If you think about it for a minute, you’ll realize that there’s nothing magical at all about having a batting average that matches a corresponding number of games.
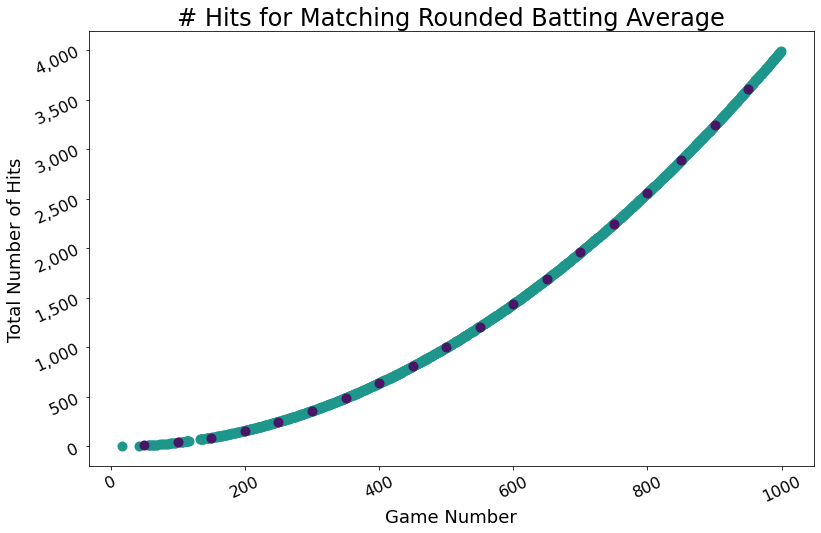
Suppose a baseball player has four at-bats per game (not including walks), so their batting average is the number of hits they got divided by four times the number of games they played. For many games, it’s possible to have a corresponding batting average that, when rounded to three digits, equals the number of games divided by 1,000. For example, if a player typically gets one hit per game in their at-bats, then they could very well have a .250 average over 250 games.
What is the greatest number of games for which it is not possible to have a matching rounded batting average? Again, assume four at-bats per game.
Solution¶
As mentioned in the description,
$$\frac{g}{4g} = .250$$
Note that
$$\frac{1}{4g} = \frac{.250}{g} = \frac{1}{1000} \cdot \frac{250}{g} < \frac{1}{1000}$$
for $g > 250$.
Since
$$\frac{g}{4g} < \frac{g}{1000}$$
it follows that there exists some integer $x$ such that
$$\frac{g}{4g} + \frac{x}{4g} \approx \frac{g}{1000}$$
This can be summarized for $h$, $g \le h < 4g$, as
$$\left \lfloor \frac{h}{4g} \right \rfloor \le \frac{g}{1000} \le \left \lceil \frac{h}{4g} \right \rceil$$
This implies every number $g > 250$ has an $h$ that produces a matching rounded batting average.
Working backwards from $g \le 249$,
| Games ($g$) |
Hits ($h$) |
Batting Avg $\left(\dfrac{h}{4g}\right)$ |
| $249$ |
$248$ |
$\dfrac{248}{996} \approx 0.249$ |
| $248$ |
$246$ |
$\dfrac{246}{992} \approx 0.248$ |
| $247$ |
$244$ |
$\dfrac{247}{988} \approx 0.247$ |
| $246$ |
$242$ |
$\dfrac{242}{984} \approx 0.246$ |
| $245$ |
$240$ |
$\dfrac{240}{980} \approx 0.245$ |
| $244$ |
$238$ |
$\dfrac{238}{976} \approx 0.244$ |
| $243$ |
$236$ |
$\dfrac{236}{972} \approx 0.243$ |
| $242$ |
$234$ |
$\dfrac{234}{968} \approx 0.242$ |
| $241$ |
$232$ |
$\dfrac{232}{964} \approx 0.241$ |
| $240$ |
$230$ |
$\dfrac{230}{960} \approx 0.240$ |