Can You Hunt For The Mysterious Numbers (IV)?¶
Riddler Express¶
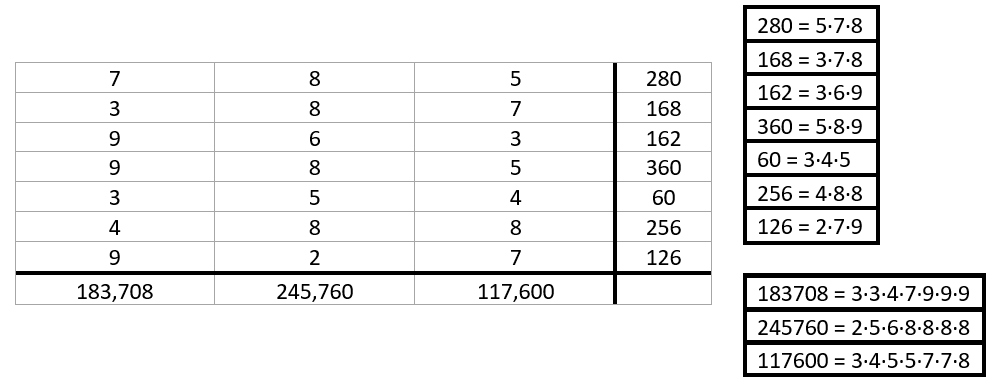
This week marks the third of four CrossProduct™ puzzles. This time, there are seven three-digit numbers — each belongs in a row of the table below, with one digit per cell. The products of the three digits of each number are shown in the rightmost column. Meanwhile, the products of the digits in the hundreds, tens and ones places, respectively, are shown in the bottom row.
Can you find all seven three-digit numbers and complete the table?
Solution¶
Step 1.¶
First, list all possibilities of products of single digits. Products that are fixed are boxed.
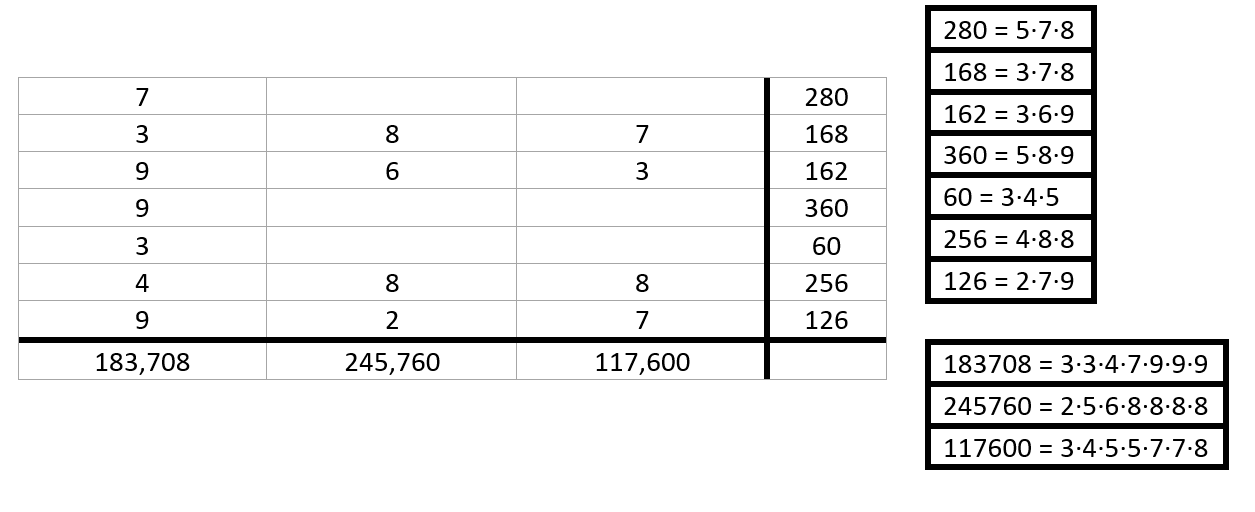
The factors of 3 have to be placed as follows, because 117,600 and 245,760 only have one each.

Step 2.¶
183,708 does not have a factor of 8. The order of 256 is set. The entire order of 183,708 is set.
The two remaining factors of 7 from 168 and 126 must be part of 117,600. The order of 168 and 162 is set.
The product of 245,760 is set. The product of 117,600 is set.
Step 3.¶
The factors of 8 from 280 and 360 must be part of 245,760. The two factors of 5 are thus a part of 117,600.
The remaining 5 from 60 must be part of 245,760.
Answer¶