Can You Win Riddler Jenga?¶
Riddler Classic¶
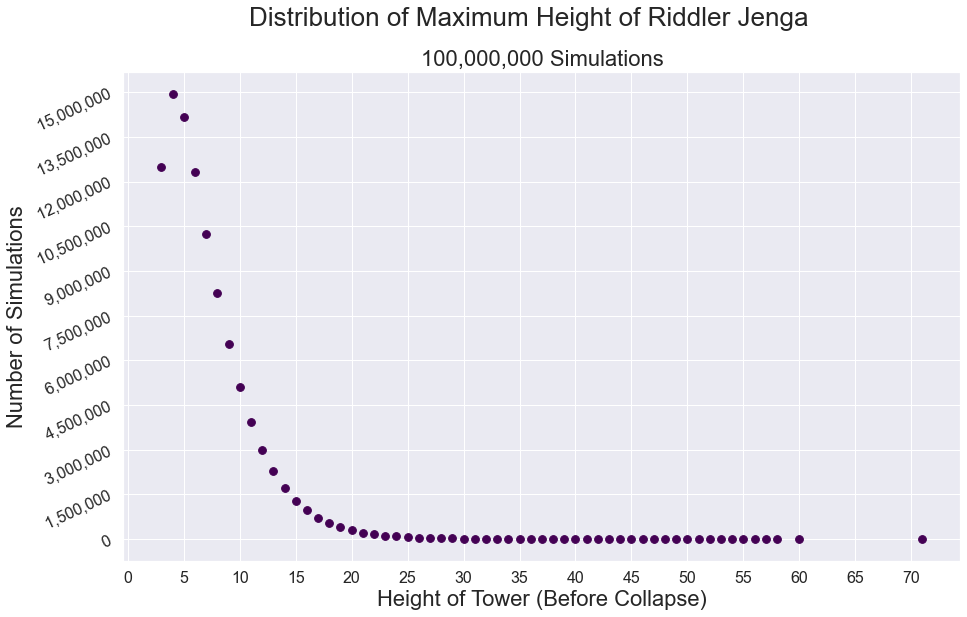
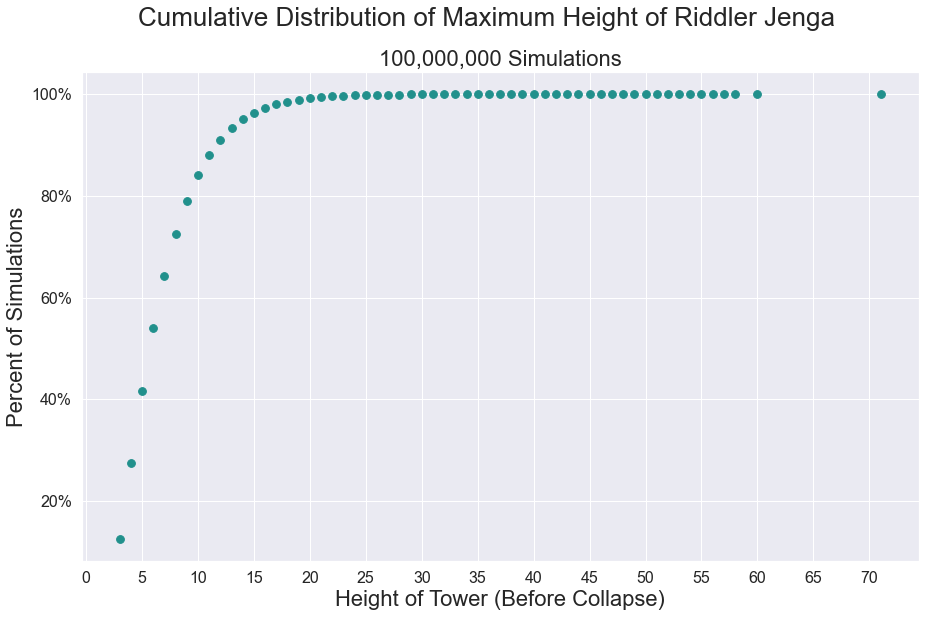
In the game of Jenga, you build a tower and then remove its blocks, one at a time, until the tower collapses. But in Riddler Jenga, you start with one block and then place more blocks on top of it, one at a time.
All the blocks have the same alignment (e.g., east-west). Importantly, whenever you place a block, its center is picked randomly along the block directly beneath it. For example, the following animation shows Riddler Jenga towers that were randomly constructed before ultimately collapsing when the fifth, 10th and 15th blocks were placed. The block highlighted in red is the one above which the blocks were no longer balanced.

On average, how many blocks must you place so that your tower collapses — that is, until at least one block falls off?
(Note: This problem is *not asking for the average height of the tower after any unbalanced blocks have fallen off. It is asking for the average number of blocks added in order to make the tower collapse in the first place.)