Can You Hunt For The Mysterious Numbers (III)?¶
Riddler Express¶
It’s the second week in our four weeks of CrossProduct™ puzzles!
This time around, there are six three-digit numbers — each belongs in a row of the table below, with one digit per cell. The products of the three digits of each number are shown in the rightmost column. Meanwhile, the products of the digits in the hundreds, tens and ones places, respectively, are shown in the bottom row.
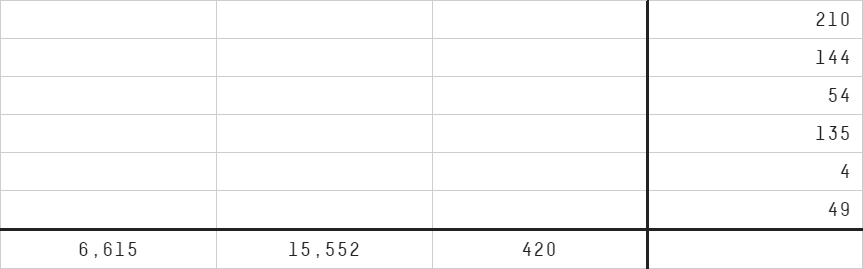
Can you find all five three-digit numbers and complete the table?
Solution¶
Step 1.¶
First, list all possibilities of products of single digits. Products that are fixed are boxed. The three 7s are fixed.
6,615 has no even factors, so it must have a 1 from 4.

Step 2.¶
The product of 6,615 is set. The two 5s are then fixed.
The 6 from 210 is fixed. The 3 and 9 from 135 are fixed, as 420 is not divisible by 9.
The product of 4 is set, as 15,552 cannot have a factor of 2. 15,552 already has a 1, so the 4 from 4 must be there.
The 8 in 15,552 must come from 144.
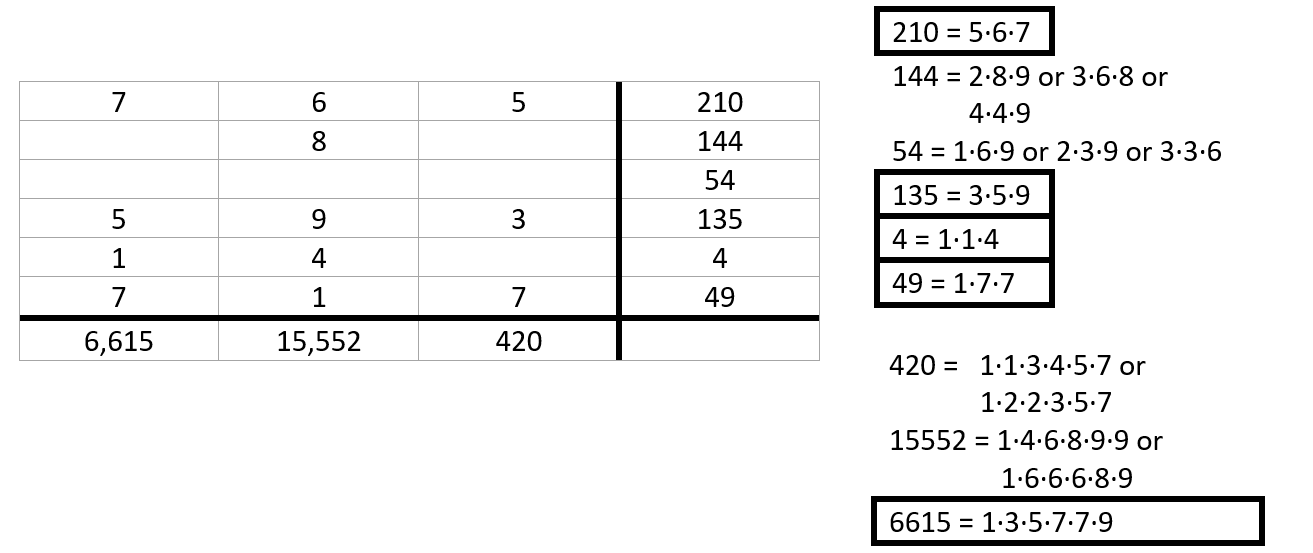
Step 3.¶
The remaining factors of 420 must be 2·2, as there are no more 4s.
The 9 from 144 is fixed. The 3 from 6,615 is fixed. The 9 from 54 is fixed.
Answer¶
