Can You Determine the Corner Distance?¶
Riddler Express¶
If you have young children (or if you’re still a child at heart), you probably have small blocks somewhere in your home.
I recently found four cubic blocks in a peculiar arrangement. Three of them were flat on the ground, with their corners touching and enclosing an equilateral triangle. Meanwhile, the fourth cube was above the other three, filling in the gap between them in a surprisingly snug manner. Here’s a photo I took of this arrangement:

If you too have blocks at home (I mean, of course you do), see if you can make the same arrangement.
Now, if each of the four cubes has side length 1, then how far above the ground is the bottommost corner of the cube on top?
Solution¶
The shape hidden from view is a triangular pyramid. The base is the equilateral triangle created by the three cubes flat on the ground. The three additional faces are from the top cube, each being an isosceles right triangle with hypotenuse $= 1$.
The height of the base is $\frac{\sqrt{3}}{2}$. The height of the triangular pyramid is from the bottom vertex to the centroid of the base triangle. The distance to the centroid is $\frac{2}{3} \cdot \frac{\sqrt{3}}{2} = \frac{1}{\sqrt{3}}$. The picture below summarizes the shape hidden from view.
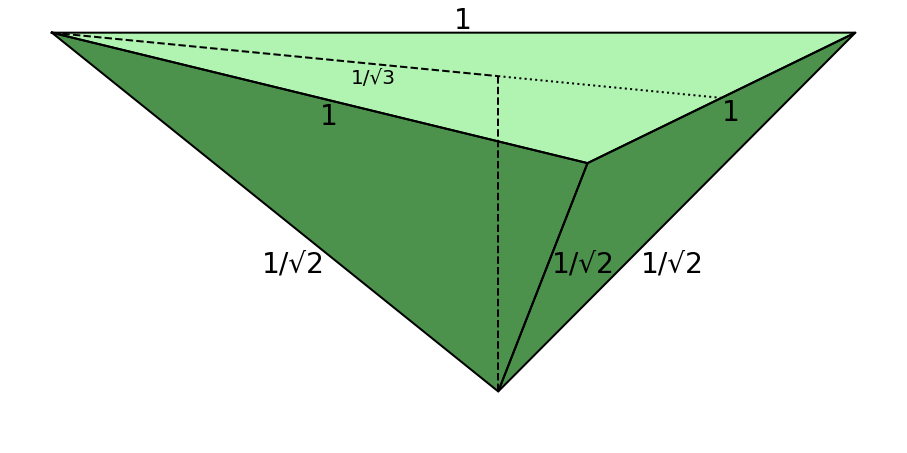
The height of the triangular pyramid is:
$$\sqrt{\left(\frac{1}{\sqrt{2}}\right)^2-\left(\frac{1}{\sqrt{3}}\right)^2}$$
$$= \sqrt{ \frac{1}{2}-\frac{1}{3} }$$
$$= \frac{1}{\sqrt{6}}$$
Answer¶
The internal diagonal of a block of side length $1$ is $\sqrt{3}$.
The distance from the ground to the top corner is thus:
$$1 + \sqrt{3} - \frac{1}{\sqrt{6}}$$
$$\approx 2.324$$
Rohan Lewis¶
2021.02.01¶
Code can be found here.