Can You Hunt For The Mysterious Numbers?¶
Riddler Classic¶
In a world of sudokus, KenKens and kakuros, Barbara Yew offers a different sort of number puzzle:
There are eight three-digit numbers — each belongs in a row of the table below, with one digit per cell. The products of the three digits of each number are shown in the rightmost column. Meanwhile, the products of the digits in the hundreds, tens, and ones places, respectively, are shown in the bottom row.

Can you find all eight three-digit numbers and complete the table? It’s a bit of a mystery, but I’m sure you have it within you to hunt down the answer!
Solution¶
Step 1.¶
First, list all possibilities of products of single digits. Products that are fixed are boxed.

Step 2.¶
The 6 from 294 must be included in 55,566. 216 is therefore 3·8·9 and 84 is therefore 3·4·7.
Look at 8, 8, 9, 9 from 8,890,560. There are only two possibilities for 9: 216 and 135. The two remaining possibilities for 8 are 112 and 40.
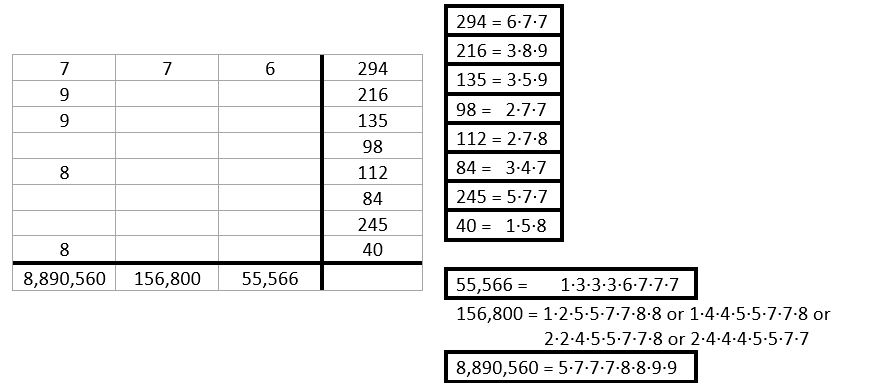
Step 3.¶
The 1 from 40 must be included in 55,566. Since the only 1 has been place and there is one 8 remaining, the product of 156,800 is set.
The 3s from 216, 135, and 84 must be included in 55,566. The remaining three boxes for 55,566 must be 7s.
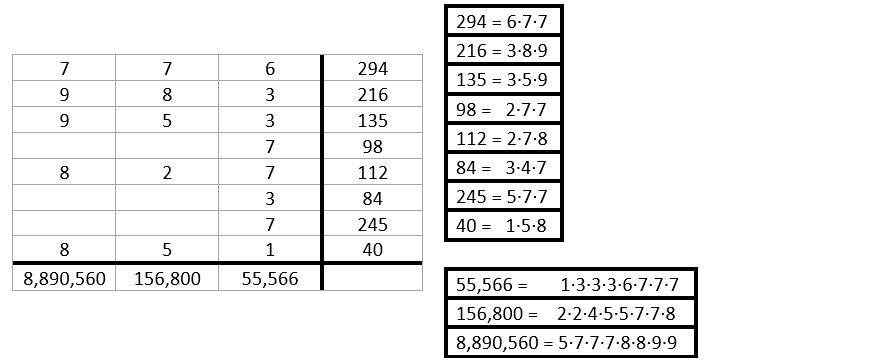
Step 4.¶
The 2 from 98 must be included in 156,800.
The 4 from 84 must be included in 156,800.
The 5 from 245 must be included in 8,890,560.
Answer¶
